Equation différentielle non linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
claudy
- Membre Naturel
- Messages: 11
- Enregistré le: 13 Sep 2015, 18:00
-
 par claudy » 08 Nov 2015, 19:02
par claudy » 08 Nov 2015, 19:02
Bonjour

Je dois trouver les fonctions y de R dans ]0;1[ dérivables sur R solutions de
(E) : y'-xy+xy^2=0j'ai pensé à diviser le tout par y^2 ce qui donne
(E) : y'/y^2 -x/y+x=0et ensuite à poser z=1/y ce qui donne
(E) : z'+xz-x=0
sauf que là je ne sais pas comment avancer sachant que une solution particulière de cette équation est z=1 mais vu l'énoncé, z ne peut être égal à 1...
Donc je pense m'être trompé avant mais je ne vois pas où...
Merci de votre aide


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Nov 2015, 19:22
par chan79 » 08 Nov 2015, 19:22
claudy a écrit: z'+xz-x=0
[/B]
sauf que là je ne sais pas comment avancer sachant que une solution particulière de cette équation est z=1 mais vu l'énoncé, z ne peut être égal à 1...
Donc je pense m'être trompé avant mais je ne vois pas où...
Merci de votre aide

Salut
Résous d'abord sans le second membre
z'+xz=0

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Nov 2015, 19:28
par zygomatique » 08 Nov 2015, 19:28
salut
ben oui z' + xz = x est une ED linéaire du premier ordre toute simple ....
il suffit donc d'ouvrir son cours ...
PS : pour diviser par un nombre il faut qu'il soit non nul
la fonction constante y = 0 est solution
on suppose ensuite que y ne s'annule pas ...
... enfin il est dit à valeur dans ]0, 1[ ... donc inutile ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
claudy
- Membre Naturel
- Messages: 11
- Enregistré le: 13 Sep 2015, 18:00
-
 par claudy » 08 Nov 2015, 19:54
par claudy » 08 Nov 2015, 19:54
Sans le second membre ça donne
=\lambda*e^{-x^2/2})
Mais le soucis vient après. Quelle solution particulière prendre vu qu'on a y de R dans ]0;1[ ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Nov 2015, 20:30
par chan79 » 08 Nov 2015, 20:30
claudy a écrit:Sans le second membre ça donne
=\lambda*e^{-x^2/2})
Mais le soucis vient après. Quelle solution particulière prendre vu qu'on a y de R dans ]0;1[ ?
Ca fait donc
=\lambda\times e^{\fra{-x^2}{2}}+1)
Trouve les valeurs de

telles que
=\fra{1}{z(x)})
soit strictement compris entre 0 et 1

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Nov 2015, 20:30
par zygomatique » 08 Nov 2015, 20:30
il faut ensuite donner la solution générale ....
et puisque le second membre est affine tu peux chercher z sous la forme affine z(x) = ax + b
z(x) = 1 est solution .. mais l'énoncé l'interdit ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
claudy
- Membre Naturel
- Messages: 11
- Enregistré le: 13 Sep 2015, 18:00
-
 par claudy » 08 Nov 2015, 20:54
par claudy » 08 Nov 2015, 20:54
Je trouve lambda strictement compris entre -

et 0 en résolvant séparément les deux inéquations y0
-
claudy
- Membre Naturel
- Messages: 11
- Enregistré le: 13 Sep 2015, 18:00
-
 par claudy » 08 Nov 2015, 21:04
par claudy » 08 Nov 2015, 21:04
chan79 a écrit:Ca fait donc
=\lambda\times e^{\fra{-x^2}{2}}+1)
Trouve les valeurs de

telles que
=\fra{1}{z(x)})
soit strictement compris entre 0 et 1
y(x) strictement inférieur à 1 équivaut à

> 1
c'est à dire à

> 0
et l'autre condition équivaut à

> -
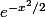
Donc, à mon avis, il faut simplement lambda strictement positif

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Nov 2015, 21:22
par chan79 » 08 Nov 2015, 21:22
claudy a écrit:y(x) strictement inférieur à 1 équivaut à

> 1
c'est à dire à

> 0
et l'autre condition équivaut à

> -
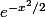
Donc, à mon avis, il faut simplement lambda strictement positif
oui, o1
-
claudy
- Membre Naturel
- Messages: 11
- Enregistré le: 13 Sep 2015, 18:00
-
 par claudy » 08 Nov 2015, 21:49
par claudy » 08 Nov 2015, 21:49
chan79 a écrit:oui, o1
Ok, merci beaucoup

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
