Bonjour,
Voici l'equadif que je dois résoudre :
(K) : y''-2y'+5y= 2e^t cos²(t) .
J'ai fais la solution de léquation homogène :
Léquation caractéristique = r²-2r+5=0
Donc ;) =-16 soit petit ;) = 2i ou -2i ainsi x1=(1+2i) et x2=(1-2i)
Ce qui me donne (K)o= ;)1e^x cos(2x) + ;)2 e^x sin(2x)
J'aimerai savoir si déjà cette réponse est juste ?
Après je suis bloquée pour la solution particulière, car on ne peut pas utiliser la décomposition de l'equadif car le résulta est un produit ...
Mais peut on dire que cos²(t)=[(1+ cos(2t)] / 2
Donc que 2e^t cos²(t) = 2.e^t . [(1+ cos(2t)] / 2 = e^t + cos(2t).e^t ?
Quelquun peut il m'aider ?
Merci d'avance
Equation différentielle 2nd degrès
12 messages
- Page 1 sur 1
Maths-ForumR a écrit:Bonjour,
Voici l'equadif que je dois résoudre :
(K) : y''-2y'+5y= 2e^t cos²(t) .
J'ai fais la solution de léquation homogène :
Léquation caractéristique = r²-2r+5=0
Donc=-16 soit petit
= 2i ou -2i ainsi x1=(1+2i) et x2=(1-2i)
Ce qui me donne (K)o=1e^x cos(2x) +
2 e^x sin(2x)
J'aimerai savoir si déjà cette réponse est juste ?
Après je suis bloquée pour la solution particulière, car on ne peut pas utiliser la décomposition de l'equadif car le résulta est un produit ...
Mais peut on dire que cos²(t)=[(1+ cos(2t)] / 2
Donc que 2e^t cos²(t) = 2.e^t . [(1+ cos(2t)] / 2 = e^t + cos(2t).e^t ?
Quelquun peut il m'aider ?
Merci d'avance
Oui, on peut. Le problème est que l'angle est encore 2t ...
Tu peux essayer la varietion des constantes.
Voici mes réponses :
1) y''-2y'+5y= e^t je trouve comme sol : 1/4 e^t
2) y''-2y'+5y= e^t[(2i+1)] je trouve : -1+(1/2) . cos (2t)
Donc une sol particulière est : 1/4 e^t + ( -1+(1/2) . cos (2t) )
Et la sol générale :
;)1e^t cos(2t) + ;)2 e^t sin(2t) + 1/4 e^t + (-1+(1/2) . cos (2t) )
Cela vous semble juste ?
1) y''-2y'+5y= e^t je trouve comme sol : 1/4 e^t
2) y''-2y'+5y= e^t[(2i+1)] je trouve : -1+(1/2) . cos (2t)
Donc une sol particulière est : 1/4 e^t + ( -1+(1/2) . cos (2t) )
Et la sol générale :
;)1e^t cos(2t) + ;)2 e^t sin(2t) + 1/4 e^t + (-1+(1/2) . cos (2t) )
Cela vous semble juste ?
salut
puisque exp' = exp j'aurais posé y(t)= z(t) exp(t)
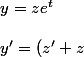e^t \\ \\ y" = (z" + 2z' + z)e^t)
alors
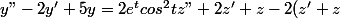 + 5z = 2cos^2t z" + 4z = 2cos^2t)
z" + 4z = 0 <== z = acos(2t) + bsin(2t)
solution particulière ::
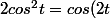 + 1)
et on peut appliquer le principe de superposition ....
pour 1 pas de problème : il suffit de prendre z = 1/4
pour cos(2t) : damned c'est déjà dans la solution homogène ....
.... mais on sait alors qu'on peut essayer une solution de la forme :
h(t) = tz(t) où z est la solution de l'équation homogène
....
puisque exp' = exp j'aurais posé y(t)= z(t) exp(t)
alors
z" + 4z = 0 <== z = acos(2t) + bsin(2t)
solution particulière ::
et on peut appliquer le principe de superposition ....
pour 1 pas de problème : il suffit de prendre z = 1/4
pour cos(2t) : damned c'est déjà dans la solution homogène ....
.... mais on sait alors qu'on peut essayer une solution de la forme :
h(t) = tz(t) où z est la solution de l'équation homogène
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Non : ça ne me semble pas juste...Maths-ForumR a écrit:Voici mes réponses :
1) y''-2y'+5y= e^t je trouve comme sol : 1/4 e^t
2) y''-2y'+5y= e^t[(2i+1)] je trouve : -1+(1/2) . cos (2t)
Donc une sol particulière est : 1/4 e^t + ( -1+(1/2) . cos (2t) )
Et la sol générale :1e^t cos(2t) +
2 e^t sin(2t) + 1/4 e^t + (-1+(1/2) . cos (2t) )
Cela vous semble juste ?
De trouver une solution particulière de ...=e^t ne donne pas d'information concernant une solution particulière de...=e^t.cos²(t)
Par contre, d'écrire le cos²(t) à l'aide de cos(2t), c'est pas con vu que ça fait apparaitre la solution générale de (E.H.)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
oui c'est bon
tu peux appliquer le principe de superposition
pour e^t cherche une solution de la forme ke^t et détermine k (tu dois trouver 1/4 comme moi)
pour e^[t(2i + 1)] essaie une solution de la forme te^[t(2i + 1)] (comme je te l'ai indiqué)
....
tu peux appliquer le principe de superposition
pour e^t cherche une solution de la forme ke^t et détermine k (tu dois trouver 1/4 comme moi)
pour e^[t(2i + 1)] essaie une solution de la forme te^[t(2i + 1)] (comme je te l'ai indiqué)
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Ah très bien excusé moi je n'avais pas bien compris ..
Oui je trouve k= 1/4 car 1 n'est pas racine de (EC)
Pour e^[t(2i + 1)] je trouve :
2i+1/4i . t.e^(2i+1)t (si je multiplie par le conjugué donc -4i) je trouve :
[(2-i)/4].t.e^(2i+1)t
Et je voulais remplacer e^(2i+1)t par : [Cos(2t) + i Sin(2t)] . e^t
Ensuite il faut prendre la partie réelle de : [(2-i)/4] . Cos(2t) + i Sin(2t) . t . e^t
Donc je trouve : (1/2 cos(2t) + 1/4 Sin(2t)) . t . e^t
Mais ça me semble faux j'aimerai avoir une confirmation
Oui je trouve k= 1/4 car 1 n'est pas racine de (EC)
Pour e^[t(2i + 1)] je trouve :
2i+1/4i . t.e^(2i+1)t (si je multiplie par le conjugué donc -4i) je trouve :
[(2-i)/4].t.e^(2i+1)t
Et je voulais remplacer e^(2i+1)t par : [Cos(2t) + i Sin(2t)] . e^t
Ensuite il faut prendre la partie réelle de : [(2-i)/4] . Cos(2t) + i Sin(2t) . t . e^t
Donc je trouve : (1/2 cos(2t) + 1/4 Sin(2t)) . t . e^t
Mais ça me semble faux j'aimerai avoir une confirmation
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
