et je dois utiliser le changement de variable
Equation differentiel Euler
8 messages
- Page 1 sur 1
Equation differentiel Euler
Bonjour, j'ai une equation differentiel à resoudre et jai de la difficulté. Jai +y=0)
et je dois utiliser le changement de variable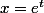 donc ln(x)=t. mon equation devient donc
donc ln(x)=t. mon equation devient donc (d^2y/dx^2)+y=0) . je sais que
. je sais que 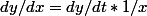 et que
et que 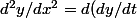/dx*1/x+dy/dt*(-1/x^2)) Et la je suis completement bloquer sur comment continuer et remplacer dans mon equations differentiel. Par la suite integrer je naurai aucun probleme.
Et la je suis completement bloquer sur comment continuer et remplacer dans mon equations differentiel. Par la suite integrer je naurai aucun probleme.
et je dois utiliser le changement de variable
Re: Equation differentiel Euler
Salut,
Perso., je me suis toujours complètement paumé avec les notations "à la physiciennes" comme celles que tu emploie où on désigne par la même lettre (en l'occurrence y) deux fonctions différentes (pour un matheux)
Bref, perso, jaurais écrit que, "poser x=e^t", ça veut dire considérer la fonction=y(e^t)) ce qui revient à écrire
ce qui revient à écrire =z(\ln(x))) .
.
Donc=\frac{1}{x}z'(\ln(x))) (dérivée d'une composée)
(dérivée d'une composée)
et=-\frac{1}{x^2}\times z'(\ln(x))+\frac{1}{x}\times \frac{1}{x}z''(\ln(x))) (dérivée d'un produit).
(dérivée d'un produit).
L'équation+y(x)=0\) s'écrit alors
s'écrit alors )+z''(\ln(x))+z(\ln(x))=0) c'est à dire
c'est à dire 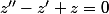 (sur
(sur 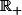 ) qui est une équation linéaire qu'on sait très bien résoudre.
) qui est une équation linéaire qu'on sait très bien résoudre.
Perso., je me suis toujours complètement paumé avec les notations "à la physiciennes" comme celles que tu emploie où on désigne par la même lettre (en l'occurrence y) deux fonctions différentes (pour un matheux)
Bref, perso, jaurais écrit que, "poser x=e^t", ça veut dire considérer la fonction
Donc
et
L'équation
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equation differentiel Euler
Bonjour !
Ajoutons que le "changement de variables" proposé suppose ce qui n'est indiqué nulle part.
ce qui n'est indiqué nulle part.
Il reste donc à résoudre l'équation sur
Ajoutons que le "changement de variables" proposé suppose
Il reste donc à résoudre l'équation sur
Re: Equation differentiel Euler
Le changement de variable que je dois utiliser est obligatoire et.les etapes que jai deja fait est le bon debut. Je dois juste continuer mais je suis bloquer je sais quil me reste 1 ou 2 etape avant de pouvoir remplacer dans mon equations et je dois avoir du y (t)
Re: Equation differentiel Euler
Obligatoire ou pas n'empêche pas de dire qu'on se place sur les réels strictement positifs.
Et être bloqué après la réponse de Ben314 ? As-tu lu cette réponse ?
Et être bloqué après la réponse de Ben314 ? As-tu lu cette réponse ?
Re: Equation differentiel Euler
Kolis a écrit:Obligatoire ou pas n'empêche pas de dire qu'on se place sur les réels strictement positifs.
Et être bloqué après la réponse de Ben314 ? As-tu lu cette réponse ?
Jai parfaitement lu par contre ou je bloque est que jai y'(x)=y'(t)*1/x et y''(x)=y''(t)*1/x^2 + y'(t)*-1/(x^2) ensuite je dois remplacer? Mais dans son equation le e^(2t) disparait. Et je remplace y (x) par quoi?
Re: Equation differentiel Euler
Tu as mal lu puisque tu continues à mélanger les ) et
et ) .
.
Il te l'a dit :=y(x)) (on a changé de fonction) et multiplier par
(on a changé de fonction) et multiplier par  (
(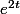 ) que tu as supposé non nul ce n'est pas une grande invention.
) que tu as supposé non nul ce n'est pas une grande invention.
Et tu te retrouves avec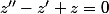 que tu sais résoudre : tu auras
que tu sais résoudre : tu auras =...) et tu en déduis
et tu en déduis ) .
.
Il te l'a dit :
Et tu te retrouves avec
Re: Equation differentiel Euler
Kolis a écrit:Tu as mal lu puisque tu continues à mélanger leset
.
Il te l'a dit :(on a changé de fonction) et multiplier par
(
) que tu as supposé non nul ce n'est pas une grande invention.
Et tu te retrouves avecque tu sais résoudre : tu auras
et tu en déduis
.
Tu as raison, jai finalement reussi mon probleme merci de votre aide!
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
