Equation différencielle d'ordre I
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kaolinoui
- Messages: 7
- Enregistré le: 24 Nov 2021, 15:51
-
 par kaolinoui » 26 Nov 2021, 20:30
par kaolinoui » 26 Nov 2021, 20:30
Bonjour, j'ai du mal à résoudre cet exercice de math avec comme énoncé :
Déterminer la fonction f, solution sur RR de l'équation différentielle :
y'=6y-8.
vérifiant f(6)=10. On notera exp(x) ou e^x pour désigner l'exponentielle de x.
f(x)=
Merci d'avance à vous pour votre aide

-
mathelot
 par mathelot » 26 Nov 2021, 20:58
par mathelot » 26 Nov 2021, 20:58
Bonsoir,
Soit l'équation
y'=ay+b
où a et b sont deux réels.
La solution y est de la forme
+Ce^{ax})
où C est un nombre réel.
cherchons la solution vérifiant
=y_0)
où

et

sont deux réels.
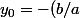+Ce^{ax_0})
soit
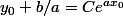
soit
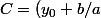e^{-ax_0})
d'où, en remplaçant C par son expression:
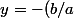+(y_0+b/a)e^{a(x-x_0)})
application:
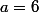
et
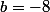
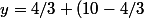e^{6(x-6)})
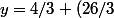e^{6(x-6)})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités