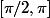oui
=-pi/2)
, je dis juste que votre dessin est bon entre [-pi,pi] et faux ailleurs, car quand vous regarder votre dessin vous voyez bien que
)
n'est pas périodique. Je m'explique :
)
est 2 pi-periodique (dixit l'énoncé) donc
=\hat f(x))
, il faut utiliser cette propriété de
)
pour construire la fonction en dehors de [-pi,pi] ,
on peut donc écrire
=\hat f(-pi/2)=-pi/2)
,
mais
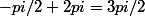
, donc
=-pi/2)
idem
)
est 2 pi-periodique donc
=\hat f(-3pi/2)=pi/2)
, car
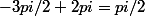
, on a
=\hat f(pi/2)=pi/2)
,
au final
=-pi/2)
et
=pi/2)
placer ces points et vous aurez le bon dessin de
)
( les autres étaient bons)
vous devriez obtenir un triangle impair.
après , vous raisonnez de la même manière, les an=0 et il faut recalculer les bn. Pour l'intégration, remarquez que
=x)
sur [0,
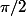
] et
=\pi-x)
sur