Equation derivee partielles

[boss201]

Soit une barre de metal de longueur 1 metre et de section constante (S) qui est tres proche de zero.La temperature a l'extremite x = 0 est maintenue a 10 degree celcius et la temperature a l'extremite x = 1 est maintenue a 90 degree celcius.La variation de temperature (θ) le long de la barre a l'instant t=0 est donne par : θ(x ,0) =50 pour 0 < x < 1.
Determiner θ(x,t). ??? La diffusivite thermique est 4m^2/s

Utiliser le changement de variable suivant : θ(x,t)=80x +10 +w(x,t).


est -ce que je peut avoir l'equation du debut et les conditions necessaire pour que je puisse commencer ce numero ?

[Yezu]

Salut;

Bonjour déjà.

Ça m'étonnerait vraiment beaucoup qu'on te balançe un problème comme ça sans que tu ne saches quelle équation différentielle modélise ce problème (à part si l'enseignant veux que vous fassiez de la recherche perso.).

[boss201]

Oui c'est un recherche personnelle , pouvez vous me donner des references ou je peut apprendre a maitriser cela ?

[pascal16]

Quand les thermomètres de précision étaient au mercure, avec une partie à l'intérieur d'un four et l'autre à l'extérieur, il y avait une correction de température à faire pour améliorer la mesure.

pour les équations, j'ai demandé à Google :
http://ressources.unisciel.fr/sillages/physique/thermo_2a_mp/res/Conduction_thermique_ESIB_MP.pdf

[Yezu]

'Équation de la chaleur' sur un moteur de recherche, et tu trouveras tout ce dont tu as besoin (:

[boss201]

'Équation de la chaleur' sur un moteur de recherche, et tu trouveras tout ce dont tu as besoin (:

Je faite des recherches sur ce que vous m'avez donner mais le truc qui est de former les conditions necessaires
(j n'arrive pas a faire pour cette cas car la temperature n'est pas constante). je serai apprecier si vous pouvez me guider sur sa.Merci


L'equation de chaleur est dθ/dt = 4[d^2θ/dx^2]

[pascal16]

θ(0 ,t) =10
θ(1,t) =90
au départ (t=0-), la barre a une température uniforme de 50° (et à t=0+, on prend 10 et 90 pour les extrémités et 50 pour le reste de la barre)
au bout d'un temps infini, l'équilibre va être une température qui croit linéairement de 10° à 90°

[LB2]

et, entre les deux, quelques oscillations ...
pour une visualisation, par exemple :
https://www.youtube.com/watch?v=b-LKPtGMdss

[boss201]

Merci a vous 2 je peut maintenant commencer la question.

[boss201]

Utiliser le changement de variable suivant : θ(x,t)=80x +10 +w(x,t).


Je n'arrive pas sa savoir ou utiliser cela ?

[GaBuZoMeu]

Tout simplement pour passer de la fonction inconnue 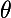à une nouvelle fonction inconnue 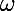vérifiant la même équation de la chaleur et ayant des conditions au bord plus sympathiques (grâce auxquelles on peut utiliser les technique habituelles)