Equation dans Z

[Sara1999]

Bonjour,
Il s’agit de prouver que l’équation: 7(x^2+y^2+z^2)(x^5+y^5+z^5)=10(x^7+y^7+z^7) , lorsque x, y et z sont des entiers relatifs tels que x+y+z≠0 n’a pas de solution.
J’ai prouvé cela si x+y+z n’est pas divisible par 7, mais je n’arrive pas à le faire dans le cas où il l’est.
Pouvez-vous m’aider? Merci.

[ComeDuRondeau]

Bonsoir,

Tu peux montrer que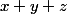 est divisible par pour dans ton exercice (pense à utiliser le petit théorème de Fermat ou le morphisme de Frobenius si tu l'as vu).

Tu devrais pouvoir conclure ensuite avec un argument de descente à l'infini !

[Sara1999]

Bonsoir,
Pour la divisibilité par 5, j’ai trouvé que x+y+z ou x^2+y^2+z^2 est divisible par 5, comment pourrai-je éliminer le second cas?
Et comment je pourrais terminer par la méthode de descente infinie, ce n’est pas encore clair pour moi. Merci .

[ComeDuRondeau]

Pardon, je n'avais pas fait attention au fait que a des solutions non triviales modulo 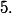Tous les triplets de la forme sont des solutions modulo .

J'ai parlé trop vite aussi pour la descente à l'infini désolé !

[Sara1999]

Pas de mal . Merci du temps que vous consacrez pour m’aider.
J’ai pensé à trouver une solution plus petite en divisant par le pgcd(x,y,z) mais le problème ici est celui des signes, car x, y et z ne sont pas forcément tous positifs ou tous négatifs.

[ComeDuRondeau]

Une façon de prouver qu'il n'existe pas de solution serait en effet de supposer que quitte à diviser par le l'équation si ce n'est pas le cas puis de prouver qu'ils ont tous un diviseur commun non trivial (ce qui serait absurde). Le mieux que j'arrive à faire c'est de montrer qu'il y a forcément une des variables divisible par et les deux autres sont premières avec
Quel est le cadre de cet exercice ? C'est un exercice de TD ?

[Sara1999]

J’ai effectivement ramené le problème au cas où pgcd(x,y,z)=1 et j’ai aussi montré que s’il y a une solution alors x+y+z est divisible par 7 grâce à Fermat. Mais la contradiction ne se montre pas .
J’ai aussi montré que (xy)^2+(yz)^2+(zx)^2 est divisible par 3 mais ça n’avance toujours pas.
L’exercice m’a été proposé par un ami étudiant .
Merci.

[Sara1999]

Pardon j’ai commis une erreur concernant (xy)^2+(yz)^2+(zx)^2, on ne peut rien dire.

[Sara1999]

Bonsoir,
S’il vous plait, si vous êtes arrivés à montrer que l’une des variables est forcément divisible par 10, et les deux autres non, cela ne montre pas par hasard, vu le fait que les 3 variables jouent un rôle symétrique, qu’elles vont être toutes les trois divisibles par 10 et avoir par là une contradiction.

[ComeDuRondeau]

Bonsoir,
S’il vous plait, si vous êtes arrivés à montrer que l’une des variables est forcément divisible par 10, et les deux autres non, cela ne montre pas par hasard, vu le fait que les 3 variables jouent un rôle symétrique, qu’elles vont être toutes les trois divisibles par 10 et avoir par là une contradiction.

Malheureusement non, ça ne montre rien. On pourrait très bien avoir solution par exemple et la symétrie du problème se manifeste alors par le fait que et les autres permutations des coordonnées sont aussi solutions.

[Sara1999]

Oui, vous avez parfaitement raison .
Cet exercice m’intrigue vraiment !

[Ben314]

Salut,
Si on pose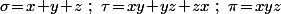 , via les identités de Newton, l'équation s'écrit
ce qui permet de simplifier par supposé non nul.
Ensuite, on peut éventuellement regarder ce que ça donne en terme d'équation (du second degré) en ou en . . .

[Sara1999]

J’ai calculé deux discriminants, mais je ne vois pas encore la contradiction, car il y a des solutions réelles lorsque x+y+z≠0 . Comment donc utiliser le fait qu’on a des entiers relatifs . Pouvez-vous me guider un peu plus, je vous en remercie.

[Sara1999]

S’il vous plait est ce qu’il n’y a aucune erreur dans la formule que vous avez trouvée ?
Merci.

[Sara1999]

Prière de me dire ce qu’il faut que je corrige dans mon raisonnement. Merci .

[Sara1999]

J’ai trouvé la même équation mais avec :
35s^3t +35 s^2t^2 où s=x+y+z et t=xy+yz+zx
J’ai calculé le discriminant pour l’équation du second degré en xyz qui est égal à :
s^2(385s^4-1470s^2t+1225t^2)
=35s^2(11s^4-42s^2t+35t^2)
Ce discriminant doit être un carré parfait, mais comment montrer que c’est impossible.
Merci.

[Sara1999]

Bonjour,
Numériquement, je trouve que l’équation
11s^2-42s^2t+35t^2=35 u^2 a toujours une solution telle que s=0 , ce qui donne la contradiction mais je n’arrive pas à le démontrer.

[catamat]

Bonjour

Vous souhaitez que 11s^4-42s^2t+35t^2 s'écrive 35(...)²

C'est un trinôme en t ,
35t²+bt+c avec b=-42s² et c=11s^4

Il s'écrira sous la forme voulue si et seulement si son discriminant est nul

Son delta vaut: 1764s^4-1540s^4 ou 224s^4

Il est nul si et seulement si s est nul ce qui est exclu...

[Sara1999]

Il y a un pb ici :
(7,42,7) vérifie cette équation !

[Sara1999]

Je crois qu’il faut abandonner le raisonnement avec le discriminant , et 35 n’est pas un carré dans Z .