L'équation de cylindre circonscrite aux sphères
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 01 Déc 2017, 06:53
par Dacu » 01 Déc 2017, 06:53
Bonjour à tous,
Déterminer l'équation du cylindre circonscrit aux sphères
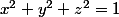
et
^2+(y+1)^2+(z-3)^2=1)
.
Cordialement,
Dacu
Modifié en dernier par
Dacu le 02 Déc 2017, 16:05, modifié 1 fois.
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Déc 2017, 07:48
par Ben314 » 01 Déc 2017, 07:48
Salut,
Un peu de bon sens, que diable !!!!!
Comment veut tu qu'un même cylindre soit circonscrit à deux sphères qui n'ont pas le même rayon !!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 01 Déc 2017, 11:01
par chan79 » 01 Déc 2017, 11:01
Salut
Lire "cône(s)" au lieu de "cylindre" peut-être ?

-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 02 Déc 2017, 16:13
par Dacu » 02 Déc 2017, 16:13
Ben314 a écrit:Salut,
Un peu de bon sens, que diable !!!!!
Comment veut tu qu'un même cylindre soit circonscrit à deux sphères qui n'ont pas le même rayon !!!!
Bonsoir,
Des milliers d'excuses!

Récitez s'il vous plaît , l'énoncé du problème...j'ai changé le rayon de la deuxième sphère.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Déc 2017, 16:41
par Ben314 » 02 Déc 2017, 16:41
Si les deux rayons sont égaux à R, le cylindre en question, c'est l'ensemble des points M qui sont à une distance R de la droite (AB) reliant les deux centres.
Donc le théorème de Pythagore nous dit que c'est les points M tels que
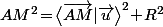
avec
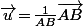
(où
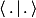
désigne le produit scalaire)
A.N. : 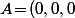\ ;\ B\!=\!(2,-1,3)\ ;\ R\!=\!1\ \Rightarrow\ x^2\!+\!y^2\!+\!z^2\!=\!\dfrac{(2x\!-\!y\!+\!3z)^2}{14}\!+\!1)
Modifié en dernier par
Ben314 le 06 Déc 2017, 19:40, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 02 Déc 2017, 17:07
par Dacu » 02 Déc 2017, 17:07
Ben314 a écrit:Si les deux rayons sont égaux à R, le cylindre en question, c'est l'ensemble des points M qui sont à une distance R de la droite (AB) reliant les deux centres.
Donc le théorème de Pythagore nous dit que c'est les points M tels que
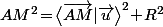
avec
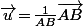
(où
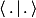
désigne le produit scalaire)
A.N. : 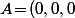\ ;\ B\!=\!(2,-1,3)\ ;\ R\!=\!1\ \Rightarrow\ x^2\!+\!y^2\!+\!z^2\!=\!\dfrac{(2x\!-\!y\!+\!3z)^2}{14}\!+\!1)
Salut,
L'équation du cylindre circonscrite aux sphères est
^2}{14}+1)
?Comment avez-vous trouvé cette équation?
Merci beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 03 Déc 2017, 10:45
par Pythales » 03 Déc 2017, 10:45
Elémentaire ...
Comme le suggère Chan79, il serait plus intéressant de chercher l'équation du cône si les sphères n'ont pas le même rayon ...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 06 Déc 2017, 09:22
par Pythales » 06 Déc 2017, 09:22
Ca n'inspire personne ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Déc 2017, 09:39
par chan79 » 06 Déc 2017, 09:39
Pythales a écrit:Ca n'inspire personne ?
salut
L'un des deux cônes a comme d'équation 9x²+12y²+4z²+4xy-12xz+6yz-4x+2y-6z=14
http://hpics.li/eff99f1

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Déc 2017, 19:39
par Ben314 » 06 Déc 2017, 19:39
Sauf erreur, des équations des cônes tangents à la sphères de centre

de rayon

et à celle de

de rayon

sont :
\big(AM^2\!-\!r^2)\!=\!\Big(\big\langle \overrightarrow{AM}|\overrightarrow{AB}\big\rangle\!-\!\ell r\Big)^{\!\!2})
avec
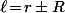
Bien sûr, si
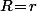
, une des deux équation, à savoir celle avec
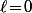
, est en fait l'équation d'un cylindre (mais l'autre avec
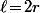
est bien l'équation d'un cône)
A.N. : 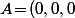\ ;\ r\!=\!1\ ;\ B\!=\!(2,-1,3)\ ;\ R\!=\!2\ \Rightarrow\ (14-\ell^2)(x^2\!+y^2+\!z^2\!-\!1)=\!\big(2x-y+3z-\ell\big)^2)
avec
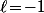
ou bien
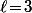
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités

avec
(où
désigne le produit scalaire)