équation complexe

[busard_des_roseaux]

bjr,

Quelqu'un peut me résoudre l'équation:



merçi d'avance.

[totom]

salut,
developpe cos(a+ib)=cos(a)ch(b)+i sin(a)sh(b), puis tu résouds l'équation,je dirais a=pi mod 2pi et b=argch(3)...bonne journée.
ps: argch(x)=ln(x+sqrt(x^2-1)), que tu peux voir comme la branche principale des logarithmes si ça t'amuse mais a et b sont reels, donc pas de determination nécessaire.
La méthode de tize redonne bien ln(3+sqrt(8))= argch(3) ouf.

[tize]

Bonjour,
une autre méthode :
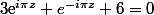
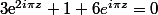
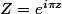
l'équation est équivalente à : qui est équivalent à après avoir multiplié par ensuite on pose et on résout l'équation du second degré...

[raito123]

Bonjours les gars,

Je veux que l'on m'explique parce que normalment dans R cette equation n'a pas de solution a car pour z reel est impossible!!!!!!

Je voudrais savoir comment ça se peut qu'elle ait des solutions en C?

C'est de quel niveau?


Merci

[tize]

Bonjour raito123,
c'est vrai la première fois ça peut choquer un peu mais c'est naturel en fait....cela vient du fait qu'au lycée on dit toujours que les fonctions sin, cos sont bornées par -1 et 1 et c'est vrai dans R mais pas dans C...
Si tu prends dans C comme définition , on peut montrer que le rayon de convergence est infini et on a même , ce qui veut dire que la fonction cos est holomorphe sur C tout entier (on dit qu'elle est entière) or le célèbre théorème de Liouville dit que toute fonction entière bornée est constante...étant donné que cos n'est pas constante c'est donc qu'elle n'est pas bornée !
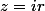
D'autre part, toujours avec cette définition on voit tout de suite qu'elle n'est pas bornée avec en faisant tendre

[raito123]

Merci tize,

Je vois les chose un peu plus claire mtn!!!

Une autre petite question : ça veut dire quoi une fonction holomorphe sur un intervalle?

Ps: Je ne connaissais pas le théorème de Liouville, merci de me l'avoir énoncer :lol4:

[busard_des_roseaux]

Bonjour,
une autre méthode :
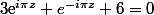
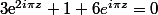
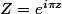
l'équation est équivalente à : qui est équivalent à après avoir multiplié par ensuite on pose et on résout l'équation du second degré...

ah oui, ok. ce que je voyais plus, c'est si j'avais besoin d'une détermination du log. En fait non, il suffit de résoudre algébriquement.

[tize]

et bien "sur un intervalle" ça ne veut pas dire grand chose car on définit plutôt les fonctions holomorphe comme étant des fonctions de ouvert de dans qui sont .
Fonction holomorphe
Théorème de Liouville

[Babe]

les fonction holomorphe sont des fonctions a variable complexe ( f(z) ), dérivable en tous les points d'un sous ensemble ouvert du plan complexe
tize arrete moi si je dis des betises

edit: bon bah mon message sert a rien :we:

[raito123]

les fonction holomorphe sont des fonctions a variable complexe ( f(z) ), dérivable en tous les points d'un sous ensemble ouvert du plan complexe
tize arrete moi si je dis des betises

edit: bon bah mon message sert a rien :we:

Si!!!!

Merci tize (et moi qui ne se douter même pas qu'il y avait une étude de l'analyse complexe:lol3:)