Équation complexe

[Rockleader]

Salut, demain j'ai DS de math sur les complexes. Et je dois dire qu'il y a certains poits du cours que je n'ai pas totalement compris...


Première chose : Concrètement qu'est ce qu'une racine n-ième de l'unité.


Seconde chose et la plus importante : Lorsque l'on cherche à résoudre une équation, admettons que l'on tombe sur un discriminant négatif, il existe donc deux racines telles que

-b + ou - i*racine de delta / 2a


D'où ma question sur un point crucial, comment peut on calculer la racines carré d'un nombre qui est négatif !



Voilà merci beaucoup de m'éclairer !

[Kikoo <3 Bieber]

Salut Rock,

D'abord, tout simplement, une racine n-ième de l'unité est une solution de l'équation :
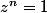avec z complexe.
L'ensemble des racine n-ièmes de l'unité se nomme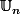 (comme dans "unité").
Après on peut dire que cet ensemble muni de la multiplication est un sous groupe du groupe qui est le groupe des complexes dont le module vaut 1, muni d'une loi multiplicative... Mais je pense que c'est secondaire.
En bref on a :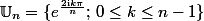

Tu as oublié de marquer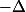 il me semble !

[Dlzlogic]

Bonjour,
Il y a bien longtemps que je n'ai utilisé les complexes, mais voila ce que je dirais pour la seconde question
Si delta est, alors D²=i² delta est positif
On peut prendre al racine de D² qui vaut i*racine(-deltaD
On a change le signe de delta parce qu'on l'a multiplié par i² = -1.

[lartdeladivisionparzero]

Salut !
Aïe. Alors les racines n-ièmes de l'unité sont les complexes b tels que b^n = 1. Il y en a une infinité et elles sont toutes sur le cercle trigonométrique de la forme exp(2i*pi*k/n) pour k relatif.
Ensuite i^2 = -1. Donc (3i)^2 = -9 (par exemple). Ce qui peut t'aider pour la résolution d'équation.
Edit : grillée sorry dlzlogic

[chan79]

Salut !
Aïe. Alors les racines n-ièmes de l'unité sont les complexes b tels que b^n = 1. Il y en a une infinité et elles sont toutes sur le cercle trigonométrique de la forme exp(2i*pi*k/n) pour k relatif.
Ensuite i^2 = -1. Donc (3i)^2 = -9 (par exemple). Ce qui peut t'aider pour la résolution d'équation.
Edit : grillée sorry dlzlogic

il n'y en a pas une infinité ...
-1 n'a que deux racines carrées (dans C) : i et -i

[Kikoo <3 Bieber]

Infinité ou pas, c'est débattable non ?

Je n'ai exhibé "que" n racines distinctes, car elles se répètent ad libitum quand k décrit Z.

Edit : finalement il se peut que nous parlions de deux choses différentes !

[lartdeladivisionparzero]

il n'y en a pas une infinité ...
-1 n'a que deux racines carrées (dans C) : i et -i

1 = e^(2ipi) = E^(4ipi) ... etc
Après oui on peut débattre du caractère infini ... disons une infinité d'écritures.

[chan79]

1 = e^(2ipi) = E^(4ipi) ... etc
Après oui on peut débattre du caractère infini ... disons une infinité d'écritures.

oui, mais à ce moment là, il y a une infinité de nombres entiers compris entre 1 et 3:
2; 4/2; 6/3; 8/4 etc :zen:

[Kikoo <3 Bieber]

Bon mettons les choses au clair :

Chan parle du fait que n n'est pas l'infini.
J'ai pensé comme "l'art de la division par 0" (grrr) qui insiste sur le fait que les racines se répètent modulo n.
Ce sont deux choses sensiblement différentes.

La base du malentendu se trouve en l'absence du mot "distinctes".

[lartdeladivisionparzero]

Je m'incline, je m'incline, il n'y en a pas une infinité :)

[Rockleader]

Donc si j'ai bien compris, la racine 3 ème de l'unité de e^6pi par exemple

Sa donnerait: e^36pi/3 = e^2pi * 18 / 3 ou alors j'ai compris de travers.



Pour la racine de delta négatif, certes pour quelque chose d'aussi simple que -4 on sait qu'on aurait 2i, c'est évident, mais si mon delta vaut disons: -5-racine de 7, ce n'est plus aussi évident

[Kikoo <3 Bieber]

oui, mais à ce moment là, il y a une infinité de nombres entiers compris entre 1 et 3:
2; 4/2; 6/3; 8/4 etc :zen:

Ce sont les même nombres, 13/6 et 1/6 ne sont pas les mêmes que je sache.

[lartdeladivisionparzero]

Donc si j'ai bien compris, la racine 3 ème de l'unité de e^6pi par exemple

Sa donnerait: e^36pi/3 = e^2pi * 18 / 3 ou alors j'ai compris de travers.



Pour la racine de delta négatif, certes pour quelque chose d'aussi simple que -4 on sait qu'on aurait 2i, c'est évident, mais si mon delta vaut disons: -5-racine de 7, ce n'est plus aussi évident

LA?? racine troisième de l'unité.
Ouille, ouille, il n'y en a pas qu'une.
Ensuite elle sont de la forme exp(2i(pi)*k/n). Pour les trouver (et qu'elles soient bien distinctes, on a vu qu'il y avait un souci ici :lol3: ), prends k de 0 à n-1

Edit : d'ailleurs les racines 3ièmes de l'unité sont notés 1, j et j^2 et tu as des propriétés sympas dessus genre 1 + j + j^2 = 0 et j^2=jbarre

[chan79]

Je m'incline, je m'incline, il n'y en a pas une infinité

pas de souci, c'est surtout que l'argument d'un nombre complexe est défini à 2 près, en radians. Infinité d'arguments, en quelque sorte

[Kikoo <3 Bieber]

Donc si j'ai bien compris, la racine 3 ème de l'unité de e^6pi par exemple

Sa donnerait: e^36pi/3 = e^2pi * 18 / 3 ou alors j'ai compris de travers.



Pour la racine de delta négatif, certes pour quelque chose d'aussi simple que -4 on sait qu'on aurait 2i, c'est évident, mais si mon delta vaut disons: -5-racine de 7, ce n'est plus aussi évident

La racine 3-ième de l'unité est la racine troisième de 1 ! L'unité c'est 1 et non pas un complexe quelconque.

Et puis oui, l'article est problématique.

[lartdeladivisionparzero]

pas de souci, c'est surtout que l'argument d'un nombre complexe est défini à 2 près, en radians. Infinité d'arguments, en quelque sorte

on est d'accord

[Kikoo <3 Bieber]

pas de souci, c'est surtout que l'argument d'un nombre complexe est défini à 2 près, en radians. Infinité d'arguments, en quelque sorte

On peut toujours se fixer à ça Ok pour un nombre fini de racines n-ième de l'unité à 2k*pi près alors !

[Rockleader]

AH daccord, il y a donc 3 racines 3ème de l'unité, plus exactement il y a n racines n-ième.


Est ce que quelqun pourrait me donner en guise d'exemple les 3 racines 3ème de l'unité pour que je vois exactement comment faire ?

[Kikoo <3 Bieber]

Edit : d'ailleurs les racines 3ièmes de l'unité sont notés 1, j et j^2 et tu as des propriétés sympas dessus genre 1 + j + j^2 = 0 et j^2=jbarre

On peut même généraliser :

, avec une racine n-ième de l'unité, pour n supérieur à 2.

[lartdeladivisionparzero]

Je viens de te donner la réponse. Tu prends les exp(2i(pi)k/n) avec n = 3 et k allant de 0 à n-1 = 2
Fais un cercle pour t'aider :)