Equation avec partie entière
17 messages
- Page 1 sur 1
Equation avec partie entière
Bonjour/bonsoir,
Je bloque sur la question suivante : Résoudre 3x² - 10E(x) + 3 = 0
Merci pour votre aide,
Akiwhite
Je bloque sur la question suivante : Résoudre 3x² - 10E(x) + 3 = 0
Merci pour votre aide,
Akiwhite
Re: Equation avec partie entière
Déjà si un tel  existe alors
existe alors  . De plus
. De plus  donc d'après la relation précédente
donc d'après la relation précédente -3< 3x^2\leqslant 10x-3) , ça doit réduire le champ des valeurs possibles pour
, ça doit réduire le champ des valeurs possibles pour  .
.
Re: Equation avec partie entière
Tuvasbien a écrit:Déjà si un telexiste alors
. De plus
donc d'après la relation précédente
, ça doit réduire le champ des valeurs possibles pour
.
Et il suffit de résoudre le trinome et de faire l'intersection avec les valeurs trouvées ? ah je crois que je dis n'importe quoi
Merci beaucoup pour ta réponse
Re: Equation avec partie entière
Tu résous les inéquations  et
et  , les solutions de
, les solutions de  sont dans l'intersection des deux intervalles précédemment trouvés, en utilisant le fait que
sont dans l'intersection des deux intervalles précédemment trouvés, en utilisant le fait que  tu n'as qu'un nombre fini de possibilités.
tu n'as qu'un nombre fini de possibilités.
Re: Equation avec partie entière
Regardons la courbe d'équation y=3x²-10x+3 ; trace cette courbe au brouillon.
Maintenant, essayons de tracer la courbe y=3x²-10E(x)+3.
Quand x est un entier, les 2 courbes coïncident.
Et quand x n'est pas un entier, E(x) est inférieur à x, et donc notre 2ème courbe est au-dessus de la parabole du début.
Tout ça, je l'exprime de façon quelconque, mais tu peux l'écrire de façon plus rigoureuse. Et quand tu auras fait le dessin, tu vas voir que c'est une très bonne base pour résoudre l'exercice.
Maintenant, essayons de tracer la courbe y=3x²-10E(x)+3.
Quand x est un entier, les 2 courbes coïncident.
Et quand x n'est pas un entier, E(x) est inférieur à x, et donc notre 2ème courbe est au-dessus de la parabole du début.
Tout ça, je l'exprime de façon quelconque, mais tu peux l'écrire de façon plus rigoureuse. Et quand tu auras fait le dessin, tu vas voir que c'est une très bonne base pour résoudre l'exercice.
Re: Equation avec partie entière
Tuvasbien a écrit:Tu résous les inéquationset
, les solutions de
sont dans l'intersection des deux intervalles précédemment trouvés, en utilisant le fait que
tu n'as qu'un nombre fini de possibilités.
Je tombe sur un intervalle [1/3 ; 3] or quand j'essaye les solutions dans Z ca ne marche pas !
Modifié en dernier par akiwhite le 02 Nov 2019, 20:05, modifié 1 fois.
Re: Equation avec partie entière
lyceen95 a écrit:Regardons la courbe d'équation y=3x²-10x+3 ; trace cette courbe au brouillon.
Maintenant, essayons de tracer la courbe y=3x²-10E(x)+3.
Quand x est un entier, les 2 courbes coïncident.
Et quand x n'est pas un entier, E(x) est inférieur à x, et donc notre 2ème courbe est au-dessus de la parabole du début.
Tout ça, je l'exprime de façon quelconque, mais tu peux l'écrire de façon plus rigoureuse. Et quand tu auras fait le dessin, tu vas voir que c'est une très bonne base pour résoudre l'exercice.
Merci, mais lorsque cette courbe est croissante, 3x²-10E(x)+3
Du coup je sais que je dois trouver 4 sol
Modifié en dernier par akiwhite le 02 Nov 2019, 21:19, modifié 3 fois.
Re: Equation avec partie entière
Attention c'est 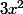 qui est entier pas
qui est entier pas  et si
et si  alors
alors  donc
donc  puis
puis  . Ca fait 27 valeurs à tester, on peut affiner en disant que
. Ca fait 27 valeurs à tester, on peut affiner en disant que  donc
donc  .
.
Re: Equation avec partie entière
Tuvasbien a écrit:Attention c'estqui est entier pas
et si
alors
donc
puis
. Ca fait 27 valeurs à tester, on peut affiner en disant que
donc
.
Effectivement ..
Re: Equation avec partie entière
Tuvasbien a écrit:Attention c'estqui est entier pas
et si
alors
donc
puis
. Ca fait 27 valeurs à tester, on peut affiner en disant que
donc
.
En fait je n'ai pas compris pourquoi
Re: Equation avec partie entière
D'accord cette partie je l'ai comprise, mais que faire après ? Il faut que je trouve 4 solutions (graphiquement j'en vois 4)
Re: Equation avec partie entière
Je confirme qu'il n'y a que 3 solutions, attention la fonction 3x^2-10E(x)+3 est pas continue donc quand la calculatrice affiche une barre verticale, en fait il n'y a rien : https://www.wolframalpha.com/input/?i=s ... 29%2B3%3D0
Re: Equation avec partie entière
Tu peux résoudre 3 ou 4 exercices consécutifs :
1. chercher des racines dans [2, 3[ ; Comme on cherche dans [2, 3[, on peut remplacer E(x) par 2. Ca donne une équation classique, on cherche ses racines, et on ne les garde que si elles sont dans [2, 3[
Et idem pour les différents intervalles qui semblent 'prometteurs'.
Je dis que tu peux faire comme ça , mais en fait, je ne vois pas d'autre méthode
1. chercher des racines dans [2, 3[ ; Comme on cherche dans [2, 3[, on peut remplacer E(x) par 2. Ca donne une équation classique, on cherche ses racines, et on ne les garde que si elles sont dans [2, 3[
Et idem pour les différents intervalles qui semblent 'prometteurs'.
Je dis que tu peux faire comme ça , mais en fait, je ne vois pas d'autre méthode
Re: Equation avec partie entière
Tuvasbien a écrit:Je confirme qu'il n'y a que 3 solutions, attention la fonction 3x^2-10E(x)+3 est pas continue donc quand la calculatrice affiche une barre verticale, en fait il n'y a rien : https://www.wolframalpha.com/input/?i=s ... 29%2B3%3D0
Ah bien vu
Re: Equation avec partie entière
Il suffit de résoudre l'équation sur les intervalles du type [k;k+1[ avec k décrivant 
Dans un tel intervalle l'équation est
Elle est équivalente à
La positivité de entraine l'absence de solutions sur
entraine l'absence de solutions sur 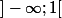
Pour k supérieur ou égal à 1 , l'équation admet au plus la solution sur [k;k+1[ .
sur [k;k+1[ .
Elle est effectivement solution ssi [k;k+1[
[k;k+1[
Soit après développement et réduction :
 et
et 
Qui est équivalent à: ET
ET 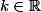
Les valeurs de k , entier , sont donc 1 , 2 , et 3 .
Les solutions correspondantes sont ,
,  , et 3 .
, et 3 .
Dans un tel intervalle l'équation est
Elle est équivalente à
La positivité de
Pour k supérieur ou égal à 1 , l'équation admet au plus la solution
Elle est effectivement solution ssi
Soit après développement et réduction :
Qui est équivalent à:
Les valeurs de k , entier , sont donc 1 , 2 , et 3 .
Les solutions correspondantes sont
Re: Equation avec partie entière
tournesol a écrit:Il suffit de résoudre l'équation sur les intervalles du type [k;k+1[ avec k décrivant
Dans un tel intervalle l'équation est
Elle est équivalente à
La positivité deentraine l'absence de solutions sur
Pour k supérieur ou égal à 1 , l'équation admet au plus la solutionsur [k;k+1[ .
Elle est effectivement solution ssi[k;k+1[
Soit après développement et réduction :et
Qui est équivalent à:ET
Les valeurs de k , entier , sont donc 1 , 2 , et 3 .
Les solutions correspondantes sont,
, et 3 .
Après avoir compris c'est plus clair comme ca, merci
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
