Équation aux dérivées partielles, changement de variable

[Wenneguen]

Bonjour,

en tant que débutant en ce qui concerne ce genre d'équations, j'aurais besoin de votre aide :

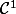
J'ai montré que est un -difféomorphisme de sur

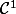
Soit de classe . On définit g sur Q' par la relation f = .
Je dois montrer que f est solution de l'équation
si et seulement si est solution d'une équation que l'on déterminera, puis trouver toutes les solutions de la première équation.

J'aurais l'idée de penser à utiliser " la règle de la chaîne " pour calculer les dérivées partielles de f par rapport à x et à y, mais je ne sais pas trop comment m'y prendre...

Merci de votre aide ! :we:

[jlb]

df/dx=dg/du *du/dx +dg/dv*dv/dx où (u,v) est l'image de (x,y) par ton C1 difféomorphisme, féomorphisme,omorphisme :we: ..

pareil pour df/dy [ produit matriciel de df et dphi]

tu formes alors l'équa diff à partir de ces nouvelles expressions et miracle tout se simplifie: il doit rester sauf erreur de ma part dg/dv=1 car xy=/0 tu intègres par rapport à v d'où g(u,v)=v + k(u)

puis tu reviens aux coordonnées initiales: f(x,y)=y²-x² +k(x²+y²) où k est une fonction C1 définie sur R+*, cela te donne la forme des solutions sur ton intervalle de défintion

[Wenneguen]

df/dx=dg/du *du/dx +dg/dv*dv/dx où (u,v) est l'image de (x,y) par ton C1...

pareil pour df/dy

tu formes alors l'équa diff à partir de ces nouvelles expressions et miracle tout se simplifie: il doit rester suf erreur de ma part dg/dv=1 car xy=/0 tu intègres par rapport à v d'où g(u,v)=v + k(u)

puis tu reviens aux coordonnées initiales: f(x,y)=x²-y² +k(x²+y²) où k est une fonction C1 définie sur R+*, cela te donne la forme des solutions sur ton intervalle de défintion

D'accord merci beaucoup je vais essayer ça !
Est-ce que tu aurais un lien où est formalisée cette règle de dérivation, parce que celle que j'ai dans mon cours me semble un peu confuse...

[jlb]

D'accord merci beaucoup je vais essayer ça !
Est-ce que tu aurais un lien où est formalisée cette règle de dérivation, parce que celle que j'ai dans mon cours me semble un peu confuse...

j'ai corrigé au dessus pour la solution ( interversion x et y)

sinon c'est l'expression des dérivées partielles d'une fonction composée, tu dois le trouver dans cours de calcul diff de base.

[jlb]

et je pense que Q' il y a un pb pour le C1 difféo,féo,o

cela ne suffit pas de regarder le jacobien ( c'est local) là il faut du global et avoir effectivement une bijection ( je pencherai pour Q'={(u,v), UdansR+* , v dans R* tq -u=
à vérifier