équation 3ème degré avec delta négatif

[Géom]

Bonjour

J'analyse des données pour un travail de fin d'étude, dont le nuage de points donne une courbe d'équation y=x².
Mon but est de mesurer la distance qui sépare chaque donnée du nuage perpendiculairement à cette courbe. Je dois donc dans un premier temps trouver les coordonnées du point d'intersection I entre la courbe et la normale à la courbe passant par mon point de donnée H. Voici un schéma de ceci :



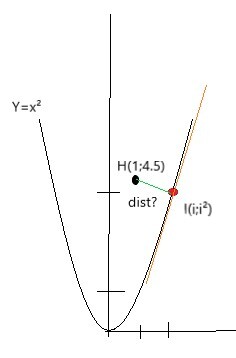
En intégrant l'équation de la normale, j'arrive à ceci :
L'objectif est de trouver i (coordonnée x de I), qui me permettra facilement de trouver la coordonnée y de I (i²).
Je dois donc résoudre cette équation de 3ème degré. Pour ce faire, j'ai trouvé la méthode de Cardan mais elle ne fonctionne que si \Delta n'est pas négatif sinon on obtient un résultat avec une racine carrée d'un nombre négatif.

Exemple : avec une donnée H (3;3,5) : devient , soit En appliquant la méthode de Cardan, j'obtiens i=2 puis i²=4, donc I(2;4) ce qui graphiquement se révèle correct. Par contre avec H(1;4,5) qui devrait aussi me donner i=2, au cours de la méthode je dois effectuer .

Comment dès lors continuer la méthode pour trouver le nombre réel 2 comme solution de l'équation ?
Sinon, y-a-t-il une autre méthode systématique (par formule applicable à Excel) pour résoudre cette équation de 3ème degré qui puisse me donner cette solution ?

D'avance merci pour vos réponses

[Black Jack]

Bonjour,

Prendre la lettre "i" comme coordonnées n'est pas recommandé (i est généralement réservé au symbole des imaginaires).

Avec I(a;a²)

L'équation de la tangente en I est : y = 2ax - a²
L'équation de la normale en I est : y = (-1/(2a))*x + a² + 1/2

La normale passe par H et donc :

yH = (-1/(2a))*xH + a² + 1/2

qui peut s'écrire : 2a³ + a.(1 - 2 * yH) - xH = 0

Par exemple avec H(1 ; 4,5), il vient : 2a³ - 8a - 1 = 0
dont la solution positive est a = 2,0597919701

Et avec H(3;3,5), il vient : 2a³ - 6a - 3 = 0
dont la solution positive est a = 1,94224185097

Ce qui ne ressemble en rien à ce que tu as fait.

Je n'ai rien vérifié, à toi de le faire si tu veux.

[Pisigma]

Bonjour à vous 2,

je trouve la même chose que Black Jack pour les 2 points H

P.S. : je suis passé par le produit scalaire

si est un vecteur directeur de la tangente en

on a

[Géom]

Rebonjour

merci à vous 2. Effectivement mon équation de base était erronée, j'ai oublié le "2" dans la dérivée... les maths sont un peu loin pour moi.

Après recalcul j'arrive aux mêmes équations pour la tangente et la normale.

Par contre, je suis toujours bloqué pour la résolution de l'équation 2a³ - 8a - 1 = 0. En appliquant Cardan j'arrive au même blocage d'une racine carré d'un nombre négatif. Comment avez-vous obtenu la solution positive ?

@Pisigma : vous avez obtenu la solution via le produit scalaire ? Si oui, pouvez-vous m'expliquer la démarche ?

Encore merci

[lyceen95]

Tu arrives aux mêmes équations pour la tangente et la normale ?
Bizarre.
Par ailleurs, avec ce point, tu vas trouver 2 points, un d'abscisse positive, et un d'abscisse négative.

[Pisigma]

, soit



un vecteur directeur de la tangente est



soit

[Black Jack]

Bonjour,

Rappel succinct de la théorie permettant de résoudre n'importe quelle
équation du type .
En posant , ces équations peuvent être ramenées à la forme :
.

3 cas peuvent alors se présenter :

1)
Il y a alors une racine réelle R.

Il y a aussi 2 racines complexes conjuguées C1 et C2.




2) .
Il y a alors une racine double .
Il y a aussi une 3ème racine : .


3) .
Il y a 3 racines réelles que l'on peut trouver par une méthode
trigonométrique.



**************************
2a³ - 8a - 1 = 0
a³ - 4a - 0,5 = 0
p = -4 et q = -0,5
... il y a donc 3 racines réelles qui sont :

[Géom]

Merci à tous pour votre aide.

Black Jack a apporté la solution que je recherchais, lorsque Delta <0, résolution que je connaissais pas et qu'il me manquait.

.
Il y a 3 racines réelles que l'on peut trouver par une méthode
trigonométrique.

Encore merci, ceci clos mon problèle