Equation du 2nd degres dans C
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 12 Nov 2014, 13:52
par Maths-ForumR » 12 Nov 2014, 13:52
Ben314 a écrit:Peut... mieux faire...
La dérivée de

est

donc, sur ]0,+oo[ le minimum est en T=1 et il vaut 2.
On peut aussi écrire (astuce)
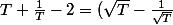^2\geq 0)
Désolé mais je ne comprend pas pourquoi on étudie la variation de T ? Pour répondre a la question montrer que b/a^2 et une quantité relle appartenant a ]0;1]

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Nov 2014, 14:28
par Ben314 » 12 Nov 2014, 14:28
Parce que
Ben314 a écrit:^2}{4z_1z_2}=\frac{( \rho+ \rho')^2e^{2i\theta}}{4\rho\rho'e^{2i\theta}} = \frac{( \rho+ \rho')^2} {4\rho\rho'}<br />=\frac{1}{4}(\frac{\rho}{\rho'}+2 + \frac{ \rho'}{\rho})<br />=\frac{1}{4}(T+2 + \frac{1}{T}))
où

et qu'on te demande de montrer que b/a^2 est dans tel intervalle.
Je sais pas comment tu t'y prend d'habitude, mais moi quand on me demande de montrer qu'un truc dépendant de T est dans un intervalle donné, ben j'étudie les variation du truc en question.
Aprés, si tu préfère, tu peut étudier

sur ]0,oo[ où tu considère
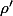
comme une constante fixée : ça te donnera évidement le même résultat.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 12 Nov 2014, 14:41
par Maths-ForumR » 12 Nov 2014, 14:41
Ben314 a écrit:Parce que et qu'on te demande de montrer que b/a^2 est dans tel intervalle.
Je sais pas comment tu t'y prend d'habitude, mais moi quand on me demande de montrer qu'un truc dépendant de T est dans un intervalle donné, ben j'étudie les variation du truc en question.
Aprés, si tu préfère, tu peut étudier

sur ]0,oo[ où tu considère
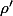
comme une constante fixée : ça te donnera évidement le même résultat.
Juste une précision vous n'avez pas inverser les valeur de b et a^2 ?
Pcq c'est b = 4z1z2 et a^2=z1+z2/4
Donc b/a^2 = 4z1z2/(z1+z2)^2 non ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Nov 2014, 14:49
par Ben314 » 12 Nov 2014, 14:49
Maths-ForumR a écrit:Juste une précision vous n'avez pas inverser les valeur de b et a^2 ?
Pcq c'est b = 4z1z2 et a^2=z1+z2/4
Donc b/a^2 = 4z1z2/(z1+z2)^2 non ?
Effectivement
J'étais parti sur le a²/b de la partie I) (et je trouve un peu con de changer dans la partie II))
D'un autre coté, ça change pas gras vu que montrer que b/a² est dans ]0,1] c'est équivalent à montrer que son inverse a²/b est dans [1,+oo[...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 12 Nov 2014, 15:02
par Maths-ForumR » 12 Nov 2014, 15:02
Oui merci
Ensuite je dois montrer que si b/a^2 alors arg(z1) congru Arg(z2)
J'ai calculé le discriminant et tombe bien sur une forme demandé :
D=4a^2y^2 avec y^2= (1-t)
Puis j'ai calculé petit delta = 2ay
Donc z1= a(1+y) et z2=a(1-y)
Ensuite il fait que je calcule :
arg(z1) = arg (a(1+y)) = arg(a) + Arg (1+y)
arg(z2) = ...................= arg(a) + arg(1-y)
Or (1+y) barre = (1-y) et arg(z)=arg(zbarre)
Soit arg(z1) congrus - arg(z2) [2Pi]
Le moins signe - ne gêne pas ?
Et cela vous semble t'il juste ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Nov 2014, 15:23
par Ben314 » 12 Nov 2014, 15:23
Non : arg(z(barre)) n'est pas égal à arg(z) (c'est l'opposé)
Et le conjugué de 1+y n'est absolument pas 1-y (y est réel !!!!)
Par contre,
Arg(1+y)=Arg(1-y)=0
vu que ce sont tout les deux des réels positifs...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 12 Nov 2014, 15:37
par Maths-ForumR » 12 Nov 2014, 15:37
Ah oui pardon..
Très bien la fin de cet exo concerne des démonstrations mais j'ai réussi a les faire :)
En tout cas MERCI BEAUCOUP pour votre aide !!
Bonne continuation
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
est
donc, sur ]0,+oo[ le minimum est en T=1 et il vaut 2.
