Equation du 2nd degres dans C
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 15:59
par Maths-ForumR » 11 Nov 2014, 15:59
Ah oui alors je ne vois pas comment avancer
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 16:20
par Maths-ForumR » 11 Nov 2014, 16:20
C'est pas plutôt ;)= Racine[(1-t)/t] sans la 4 ?
Car D =4a² - (4a²/t) = -4a² ((1/t)-1) = -4a² ((1+t)/t)
donc ;)²=((1+t)/t) et ;)= Racine[(1-t)/t] ?
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 16:53
par Maths-ForumR » 11 Nov 2014, 16:53
Et je ne vois pas très bien quel est le but de cette indication :/
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 16:54
par Maths-ForumR » 11 Nov 2014, 16:54
Et je ne vois pas très bien quel est le but de cette indication ? :/

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 17:36
par Ben314 » 11 Nov 2014, 17:36
Maths-ForumR a écrit:C'est pas plutôt

= Racine[(1-t)/t] sans la 4 ?
Si, (mais en fait le 4 on s'en fout...)
Concernant la suite, tu as du voir en cours que les racines de ton équation sont

où

est une des racines carrés de

donc ici, on peut prendre

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 17:49
par Maths-ForumR » 11 Nov 2014, 17:49
Dans mon cours les racines sont (2a+-d)/2 et non sur 4
Et je ne comprend pas trop la méthode pour trouver petit delta

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 18:02
par Ben314 » 11 Nov 2014, 18:02
Tu as raison concernant le 4.
Après, comment je trouve le

....
Ben je regarde
droit dans les yeux l'expression

, puis j'incante une formule de magie (noire bien sûr, donc je peut pas la répéter) et là, dans les brumes profonde de mon cerveau apparait (entre deux dent de Furet) la formule
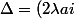^2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 18:08
par Maths-ForumR » 11 Nov 2014, 18:08
Oula oui pardon le (-1)=i² merci :)
Donc après on remplace petit delta dans (2a+-d)/2
On obtient z1 et z2
Peut on faire z2 = -z1 et que lz1l = l-z1l donc que lz1l = lz2l
Peut on faire ça ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 18:17
par Ben314 » 11 Nov 2014, 18:17
Non, ils ne sont pas conjugués à cause du facteur a qu'il y a devant qui n'est pas forcément réel.
Mais par contre le facteur a ne change rien concernant les modules de z1 et z2 (qui sont égaux) vu que le module d'un produit est égal au produit des modules.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 18:23
par Maths-ForumR » 11 Nov 2014, 18:23
Donc je peux écrire :
lz1l = la(1+;)i)l = lal x l1+;)il
lz2l = la(1-;)i)l = lal x l1-;)il
Or l1+;)il = l1-;)il donc lz1l = lz2l ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 18:38
par Ben314 » 11 Nov 2014, 18:38
oui, c'est ça.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 18:40
par Maths-ForumR » 11 Nov 2014, 18:40
Ah super merci !!
Par contre pour 1-B.d) Donner une condition nécessaire et suffisante sur les coefficients a et b pour que module z1 = module z2 il faut faire des calculs ou c'est une reponse immédiate ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 18:54
par Ben314 » 11 Nov 2014, 18:54
C'est exactement ce qu'on vient de faire (les deux implications)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 19:12
par Maths-ForumR » 11 Nov 2014, 19:12
Donc je peut mettre que a = bt avec t réel appartenant ]0;1] ?
Pour la 2) il faut montrer que pour tout (x,y) appartenant (R+)², Racine(xy)<= (x+y)/2
Donc je voulais dire que en vue du domaine de définition :
Racine(xy)<= (x+y)/2 est rangé dans la même ordre que leur carré donc on passe l'expression au ² .
Donc : xy<= (x+y)²/4 puis je trouve en fin de calcul :
(x-y)²>=0 ce qui est vrai pour tout (x,y) appartenant (R+)²
Donc l'expression est démontrée.
Cela semble t-il correct ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 19:42
par Ben314 » 11 Nov 2014, 19:42
Maths-ForumR a écrit:Donc je peut mettre que a = bt avec t réel appartenant ]0;1] ?
que
a²=bt (c'est a²/b qui doit être réel entre 0 et 1)
Pour l'autre exo. c'est tout bon...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 20:32
par Maths-ForumR » 11 Nov 2014, 20:32
Ah oui merci !!
Pour 2) b- On suppose que Arg(z1) congru/ Arg(z2) [2Pi]
Écrire z1 et z2 sous forme expo puis en déduire la forme expo de b/a²
En déduire que b/a² est une quantité réelle appartenant a ]0;1]
ça ressemble a la première partie mais je n'arrive pas a le faire, une aide ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 21:11
par Ben314 » 11 Nov 2014, 21:11
C'est le même principe...

;

^2}{4z_1z_2}=\frac{( \rho+ \rho')^2e^{2i\theta}}{4\rho\rho'e^{2i\theta}} = \frac{( \rho+ \rho')^2} {4\rho\rho'}<br />=\frac{1}{4}(\frac{\rho}{\rho'}+2 + \frac{ \rho'}{\rho})<br />=\frac{1}{4}(T+2 + \frac{1}{T}))
où

Et si tu étudie les variations de

sur ]0,+oo[ tu verra que c'est toujours >= ???
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Maths-ForumR
- Membre Relatif
- Messages: 462
- Enregistré le: 24 Jan 2014, 18:42
-
 par Maths-ForumR » 11 Nov 2014, 22:04
par Maths-ForumR » 11 Nov 2014, 22:04
On trouve que c'est >= a 0 ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Nov 2014, 09:03
par Ben314 » 12 Nov 2014, 09:03
Peut... mieux faire...
La dérivée de

est

donc, sur ]0,+oo[ le minimum est en T=1 et il vaut 2.
On peut aussi écrire (astuce)
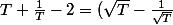^2\geq 0)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 12 Nov 2014, 09:09
par mathelot » 12 Nov 2014, 09:09
.................................................
:doh:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
= Racine[(1-t)/t] sans la 4 ?
 ....
.... , puis j'incante une formule de magie (noire bien sûr, donc je peut pas la répéter) et là, dans les brumes profonde de mon cerveau apparait (entre deux dent de Furet) la formule
, puis j'incante une formule de magie (noire bien sûr, donc je peut pas la répéter) et là, dans les brumes profonde de mon cerveau apparait (entre deux dent de Furet) la formule 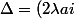^2)
