équadiff toute bête ms énervante ^^

[Matilde]

bonjour,
on me demande de résoudre cette equadiff sur IR:
(1) xy'-y=-x²e^x

d'abord, on me la fait résoudre sur IR*, et j'obtiens :
f(x)=kx-xe^x, avec k réel, et l'on me demande ensuite:

chercher les solutions définies sur IR de (1) à partir de f(x), et là, je ne sais pas comment m'y prendre, étant donné que quand je dérive cette fonction et que je la remplace dans (1), j'obtiens -x²e^x, alors qu'il me faut obtenir une constante.
pourriez-vous m'aider s'il vous plait?
merci d'avance !^^
mat

[jose_latino]

Alors, tu peux considérer maintenant la solution sur 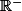, celle-ci est , pour quelque constante .

Si un fonction safistait l'équation différentielle, ça veut dire que sur 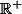a la forme et de façon analogue pour 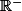, a la forme . Tu as comme condition que la fonction est dérivable en 0 (alors est continue en 0 aussi). Pour la continuité, tu as que . Essaye que analyser le limite de la dérivé et cherche les conditions pour que celui-ci existe. :zen: