Equa. diff.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Polly
- Membre Naturel
- Messages: 53
- Enregistré le: 17 Sep 2007, 17:07
-
 par Polly » 28 Jan 2008, 19:07
par Polly » 28 Jan 2008, 19:07
Bonsoir...
En pleines révisions des équa. diff., je me posais une question ...
Dans le cas des équa. diff. linéaires d'ordre 1, connaissant une solution particulière de l'équation homogéne associée
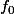
, comment sait-on que la solution sera de la forme
= f_0(x) * u(x))
...
Je recherche la preuve...
Merci d'avance!
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 28 Jan 2008, 21:38
par BertrandR » 28 Jan 2008, 21:38
Bonsoir,
Il me semble que tu fais une confusion entre plusieurs choses...
D'abord une equation différentielle linéaire homogène (c-a-d sans second membre) admet une solution générale f(x). (En exponentielle d'ailleurs). On parle de solution particuliere quand il y a un second membre.
Ensuite une fois que tu as une solution, tu les as toutes. Pourquoi ? Parce que l'ensemble des solution d'une équation différentielle linaire d'ordre n forme un espace vectoriel de dimension n (C'est une des théoreme de Cauchy il me semble, ou d'un autre sur la dimension de l'espace engendré par les solutions.). En tant qu'espace vectoriel, Il suffit d'en connaitre le même nombre de solution que la dimension de l'espace engendré, auquel cas tu as toutes les autres par combinaison linéaire. En gros c'est cas. Tu n'as pas préscisé ton niveau, mais si tu est avant le bac, ne tient pas compte de cela, admet que quand tu as une solution d'une equa diff linéaire d'ordre 1, tu as toutes les solutions.
Byebye
 par busard_des_roseaux » 29 Jan 2008, 07:48
par busard_des_roseaux » 29 Jan 2008, 07:48
bjr,
de plus, si f est solution générale de l'équation sans second membre, on cherche une solution particulière de l'équation avec second membre sous la forme y(x)=k(x)f(x). c'est la méthode de "variation de la constante".
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités