bonjour,
Pouvez-vous m'expliquer comment trouver les racines de l'équation z'+z=xexp(ix).
On doit trouver z(x)= (x/(1+i)-1/(1+i)²)exp(ix) qui se simplifie en ((1-ix)/2+i/2)exp(ix) mais je ne sais pas comment... si quelqu'un a une idée, d'avance merci !
Equa diff
6 messages
- Page 1 sur 1
par Ben314 » 15 Oct 2010, 12:30
Y'a un truc que je capte pas trop :
dans "l'équation" z'+z=xexp(ix), c'est qui l'inconnue ? qui est connu ?
Si l'inconnue est z et que x et z' sont connu, je voterais bien pour z=xexp(ix)-z' comme solution...
Ou alors c'est une équation différentielle où l'inconnue z est une fonction de t ?
Mais ça ne peut pas être ça non plus vu que, dans ce cas, il y aurait une infinité de fonction z solution...
dans "l'équation" z'+z=xexp(ix), c'est qui l'inconnue ? qui est connu ?
Si l'inconnue est z et que x et z' sont connu, je voterais bien pour z=xexp(ix)-z' comme solution...
Ou alors c'est une équation différentielle où l'inconnue z est une fonction de t ?
Mais ça ne peut pas être ça non plus vu que, dans ce cas, il y aurait une infinité de fonction z solution...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par mathelot » 15 Oct 2010, 12:40
ben,
z est l'inconnue, c'est une fonction de la variable réelle
, à valeur dans C
l'équa diff se sépare en deux équations différentielles habituelles
'(x)+\Re(z)(x)=x cos \,x)
'(x)+\Im(z)(x)=x sin \,x)
par exemple=sin(1+ix))
qui a pour partie réelle
(x)=sin(1) \, e^x)
sauf erreur de calcul
et au lieu de travailler sur deux fonctions réelles (=double de boulot)
on passe par C avant de projeter sur les axes R et iR
remarque on utilise la dérivation complexe (holomorphe) pour effectuer deux dérivations réelles à la fois
le cadre général , c'est de considérer une courbe du plan complexe C1 paramétrée par
)
puis de composer par une fonction holomorphe f
alors les choses marchent bien car la dérivée de
))
est
 \times \alpha'(x)))
z est l'inconnue, c'est une fonction de la variable réelle
l'équa diff se sépare en deux équations différentielles habituelles
par exemple
qui a pour partie réelle
et au lieu de travailler sur deux fonctions réelles (=double de boulot)
on passe par C avant de projeter sur les axes R et iR
remarque on utilise la dérivation complexe (holomorphe) pour effectuer deux dérivations réelles à la fois
le cadre général , c'est de considérer une courbe du plan complexe C1 paramétrée par
alors les choses marchent bien car la dérivée de
est
par Phile » 15 Oct 2010, 20:15
un grand merci à toi mathelot pour tes réponses, mais comment fais-tu pour obtenir les solutions de z explicitées plus haut ? Je ne parviens pas à retrouver la forme de z(x)...
par mathelot » 16 Oct 2010, 04:53
Bonjour,
i) avec la méthode de "variation de la constante"
=xe^{(1+i)x})
que l'on intégre par partie, comme pour une exponentielle réelle, avec le facteur complexe constant
)
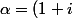ii) en cherchant a priori une solution particuliere
de la forme
e^{ix})
a et b étant complexes
on identifie alors les coefficients de fonctions polynômes,issues de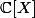
de la variable réelle (il y a de quoi y perdre son latin)
i) avec la méthode de "variation de la constante"
que l'on intégre par partie, comme pour une exponentielle réelle, avec le facteur complexe constant
ii) en cherchant a priori une solution particuliere
de la forme
on identifie alors les coefficients de fonctions polynômes,issues de
de la variable réelle
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :