Equa diff' du second ordre à coeficients variables
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zouizzzz
- Messages: 6
- Enregistré le: 29 Aoû 2006, 17:52
-
par Zouizzzz » 14 Oct 2006, 15:09
Bonjour, je bloque sur la résolution de cette équation différentielle :
y"-xy'-4y=0)
sur
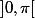
L'intervalle et le coeficient de la dérivée seconde m'ont fait penser au changement de variable
)
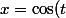J'ai donc :
)' = -\sin(t)y'(\cos(t)))
)" = -\cos(t)y'(\cos(t)) + \sin(t)^2y"(\cos(t)))
^2=sin(t)^2)
Et l'équation devient :
^4y"(\cos(t)) -\cos(t)\sin(t)^2y'(\cos(t)) + \cos(t)\sin(t)y'(\cos(t)) -4y(cos(t)) = 0)
J'ai espéré un moment que les y' s'annuleraient, mais non il y a un sinus carré... :mur: Je ne vois pas trop comment faire pour me ramener à une équation du second ordre que je puisse résoudre (i.e. linéaire et à coefs constants).
Merci d'avance.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
par alben » 14 Oct 2006, 16:41
bonjour,
Je pense que ton idée de départ était la bonne mais que tu t'es embrouillé dans les calculs en inversant les dérivées par rapport à x et celles par rapport à t.
Par ailleurs, la dérivée de cost c'est -sint !
Sinon, il me semble que ton changement de variable conduit à
Sauf erreur de calcul
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
