Bonjour,
Voici le début d'énoncé d'un exercice extrait du concours ITPE 2007 :
On considère l'équation différentielle :
(1) y"- 2by' + (a^2 + b^2)y = 0
où a et b sont deux réels connus et y une fonction inconnue de la variable réelle x.
I.1. Déterminer les solutions de l'équation différentielle (1). -> OK
I.2.a. Chercher les fonctions y solutions de (1) telles que y(0) = 1 et y0(0) = b . -> OK
I.2.b. Chercher les fonctions y solutions de (1) telles que y(0) = 0 et y0(0) = a . -> OK
I.3. Donner une condition nécessaire et suffisante qui porte sur les réels a et b pour que l'équation différentielle (1) admette des solutions paires non nulles ?
Je suis coincée à cette question : quelqu'un aurait-il des éléments de réponse?
Merci. :id:
Equa diff extrait concours ITPE
5 messages
- Page 1 sur 1
salut,
il me semble qu'on a
avec et
et  que tu détermines avec les conditiones initiales,
que tu détermines avec les conditiones initiales,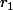 et
et 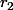 les solutions de ton equation du polynome caractéristique.
les solutions de ton equation du polynome caractéristique.
Si jamais ya que une seule solution, ya quelquechose du style
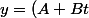e^{rt})
Donc :
si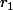 et
et 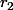 sont réelles : on aura pas une fonction paire
sont réelles : on aura pas une fonction paire
si est unique, pareil
est unique, pareil
si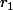 et
et 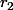 sont complexes conjuguées (a et b donnés réels), on peut réécrire y sous la forme
sont complexes conjuguées (a et b donnés réels), on peut réécrire y sous la forme
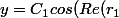t)+C_2sin(Im(r_1)t))
La ya des fonctions paires non nulles
il me semble qu'on a
avec
Si jamais ya que une seule solution, ya quelquechose du style
Donc :
si
si
si
La ya des fonctions paires non nulles
la vie est une fête 
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
