Epigraphe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 31 Mai 2010, 19:21
par AceVentura » 31 Mai 2010, 19:21
Bonsoir,
je cherche à prouver que f est convexe si et seulement si son épigraphe est une partie convexe de

.
(

)
Il faut prouver que si
)
alors
)
.
On muni donc

d'un repère (quelconque ? orthonormal ? orthogonal ?) et on considère
)
avec
)
et
)
.
Si

, que vérifient les coordonnées
)
d'un tel point et pourquoi ?
Merci par avance.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 31 Mai 2010, 19:50
par Joker62 » 31 Mai 2010, 19:50
Haileau !
On a f(a) <= b ; f(c) <= d par définition de l'épigraphe.
Si T(x,y) est sur le segment [MN]
On l'écrit T = Lambda*M + (1-Lambda)N
Donc x = Lambda*a + (1-Lambda)c
y = Lambda*b + (1-Lambda)*d
Maintenant il reste à montrer que f(x) <= y pour que T soit dans l'épigraphe.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 31 Mai 2010, 20:30
par AceVentura » 31 Mai 2010, 20:30
T = Lambda*M + (1-Lambda)N
Cela signifie quoi cette écriture ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 31 Mai 2010, 20:38
par Doraki » 31 Mai 2010, 20:38
Si T est sur le segment NM, ça veut dire qu'il existe un réel lambda entre 0 et 1 tel que le vecteur NT = lambda * le vecteur NM.
Quelle est ta définition de "f est convexe" ?
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 31 Mai 2010, 20:41
par AceVentura » 31 Mai 2010, 20:41
Doraki a écrit:Si T est sur le segment NM, ça veut dire qu'il existe un réel lambda entre 0 et 1 tel que le vecteur NT = lambda * le vecteur NM.
Pourquoi ?
Sinon pour la définition, f est convexe sur un intervalle I si
\in I^2)
,
y)\le tf(x)+(1-t)f(y))
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 31 Mai 2010, 21:17
par Doraki » 31 Mai 2010, 21:17
Tu as quelque part la définition d'un segment ?
Si A et B sont deux points du plan,
la droite (AB) est l'ensemble des points C tels que le vecteur AC est colinéaire au vecteur AB.
C'est à dire l'ensemble des points C tels que AC = k * AB, avec k dans R.
si k=0, C=A.
si k=1, C=B.
Si k est entre 0 et 1, C est entre A et B, c'est à dire C est sur le segment AB.
Si k est négatif, ou plus grand que 1, C se retrouve à l'extérieur du segment.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 31 Mai 2010, 21:40
par AceVentura » 31 Mai 2010, 21:40
Oui, j'ai noté
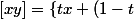y\:\:t\in [0,1]\})
. Maintenant, c'est vrai que vectoriellement, ce que tu as dit me semble logique ! Je ne sais pas ce qui est de rigueur.
Donc y'a plus qu'à passer aux coordonnées !
Mais pour la réciproque

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Juin 2010, 09:27
par Doraki » 01 Juin 2010, 09:27
La réciproque est un peu plus simple que le sens direct.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 01 Juin 2010, 10:42
par AceVentura » 01 Juin 2010, 10:42
Il faut que je détermine une équation de la droite (AB) ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Juin 2010, 11:00
par Doraki » 01 Juin 2010, 11:00
Euh.. tu parlais de la réciproque de quoi ?
je pensais à la réciproque de f est convexe <=> l'épigraphe de f est convexe.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 01 Juin 2010, 11:56
par AceVentura » 01 Juin 2010, 11:56
Oui, c'est bien celle-ci ! Le segment [AB] est inclus dans Epi(f), si A et B sont dans Epi(f). Il faut alors prouver que f est convexe. Je vais essayer de montrer que la courbe de la restriction de f à [a,b] est en-dessous de la droite [AB], non ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 01 Juin 2010, 12:21
par Doraki » 01 Juin 2010, 12:21
En-dessous du segment [AB] où A est le point (a,f(a)) et B est (b,f(b)) ?
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 01 Juin 2010, 13:55
par AceVentura » 01 Juin 2010, 13:55
Oui, c'est bien ça. Est-ce correct ? Il me semble que ça marche. Quel était ton idée ?
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 02 Juin 2010, 21:13
par AceVentura » 02 Juin 2010, 21:13
Qu'en penses-tu Doraki ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Juin 2010, 10:32
par Doraki » 03 Juin 2010, 10:32
Oui il faut faire comme ça mais j'aimerais que tu détailles un peu le raisonnement.
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 03 Juin 2010, 12:55
par AceVentura » 03 Juin 2010, 12:55
Je ne suis pas certain de l'utilisation du fait que Epi(f) soit convexe : elle intervient dans le fait que si A et B sont dans Epi(f) (ici on a pris le cas particulier ou ces points étaient même sur la courbe de f) alors
)
et donc tout point du segment est dans Epi(f).
Qu'en penses-tu ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Juin 2010, 14:36
par Doraki » 03 Juin 2010, 14:36
Oui, comme les points A et B de coordonnées (a,f(a)) et (b,f(b)) sont dans Epi(f), qui est convexe, le segment [AB] y est aussi :
Donc pour tout t dans [0;1], le point de coordonnées (ta+(1-t)b, tf(a)+(1-t)f(b)) est dans Epi(f).
Donc pour tout t dans [0;1], f(ta+(1-t)b) <= tf(a)+(1-t)f(b).
 par alavacommejetepousse » 04 Juin 2010, 10:58
par alavacommejetepousse » 04 Juin 2010, 10:58
Doraki a écrit:Euh.. tu parlais de la réciproque de quoi ?
je pensais à la réciproque de f est convexe l'épigraphe de f est convexe.
bonjour
pour moi c'est la définition de convexe
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 04 Juin 2010, 11:27
par AceVentura » 04 Juin 2010, 11:27

définie sur

est convexe lorsque
y)\le tf(x)+(1-t)f(y))
. Après, chacun sa définition.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités