3 entiers en 1

[Imod]

Oui alben je suis d'accord pour le côté évident de l'injection mais la surjectivité me gène beaucoup plus , peut être que je passe à côté de quelque chose d'évident ?

Imod

[alben]

Je ne vois pas de méthode qui ne revienne pas à exhiber l'antécédant d'un rationnel. Et pour cela, je ne peux pas éviter les puissances de 2 (ou l'écriture en binaire, ce qui revient au même).
J'ai essayé si l'on ne pouvait pas montrer globalement la surjectivité avec Bezout mais sans succès. On retombe sur l'algorithme d'Euclide généralisé.
Toutefois, le calcul de l'antécédent à partir d'une suite double finie n'est pas bien complexe.
:id: On peut peut-être en posant
[TEX]A=\{q\in N |\exist p\in N \; pgcd(p,q)=1\; et \; p contradiction...

[Imod]

Encore une fois d'accord à 100% avec ce que tu dis , j'ai aussi utilisé une interprétation qui se ramène à une décomposition en base 2 pour faire apparaître une contradiction sur l'existence d'un maximum d'un ensemble qui s'apparente au tien . C'est quand j'ai voulu mettre au propre les "on voit bien que " et les "il est clair que" que j'ai tenté une nouvelle approche mais je me suis peut être enfermé dans un rigorisme inutile . Je poste ma solution dès que j'aurais trouvé un moment pour la taper .

En tout cas merci de t'intéresser au problème :we:

Imod

[alben]

Mais non, la dernière démarche dont j'ai eu l'idée en rédigeant le post marche parfaitement :

1. N* est inclus dans f(N*) puisque f(2^k)=k
2. on définit
   En d'autres termes
3. On généralise à Q* par division euclidienne en utilisant le point 1

Voilà une démo qui me semble à peu près exhaustive et qui n'est pas très lourde.
Est-ce la tienne ?

PS ton équation me rappelle de vieux souvenirs. Je ne lache pas l'affaire mais je n'ai pas trouvé le temps de m'y remettre :we:

[Imod]

Désolé alben , soit je prends un moment pour tapper mon texte soit je lis le tien , j'ai choisi la première solution mais je te lis demain bien sûr .
A la fonction f on associe un arbre de sommet principal f(1)=1 et chaque sommet génère deux fils , l'ainé f(2n) et le cadet f(2n+1) . L'ensemble des sommets est clairemant en bijection avec N* car chaque génération comporte éléments : . Par construction le fils ainé de a/b est (a+b)/b et le cadet b/(a+b) . Réciproquement , si a/b est un fils , il est l'ainé de (a-b)/b ou le cadet de (b-a)/a .
On vérifie facilement que les fractions qui définissent les différents enfants sont irréductibles , que les ainés sont supérieurs à 1 , que les cadets sont inférieurs à 1 et que deux frères sont inverses l'un de l'autre .

1°) Tout rationnel positif apparaît dans l'arbre .

Supposons par l'absurde qu'il existe des rationnels positifs a/b n'apparaissant pas dans l'arbre , considérons parmi eux ceux qui ont un dénominateur minimal et parmi eux celui dont le numérateur est minimal .

- Si a<b alors (a+b)/a figure dans l'arbre et c'est un fils ainé . Le frère de son père est a/b . Contradiction .
- Si b<a alors (a-b)/a figure dans l'arbre ainsi que son fils ainé a/b . Contradiction .

2°) Aucun rationnel n'apparaît deux fois .

Toujours par l'absurde , s'il existe des rationnels a/b qui apparaîssent deux fois , on considère le plus petit ( au sens du 1°)

- Si a<b , a/b est un cadet , son père (b-a)/a figure aussi deux fois . Contradiction .
- Si b<a , a/b est un ainé , son père (a-b)/b figure aussi deux fois . Contradiction .

Le bref coup d'oeil que j'ai posé sur ton texte me dis que nous allons dans le même sens , mais j'ai toujours adoré "habiller" les exercices pour mieux les assimiler ( mon niveau d'abstraction atteind vite ses limites ) . A demain , ou plutôt à tout à l'heure , je n'avais pas vu l'heure et à huit heures au travail !

Imod

[alben]

Suite : fonction réciproque:
La démo du fait que la fonction est bijective n'est pas suffisante pour les casseurs de codes et autres hackers. Il faut expliciter la fonction réciproque :
1 démarche avec les fractions continues
Soit y un rationnel que l'on développe en fraction continue sous la forme

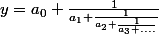
Ce développement est fini car y est un rationnel, soit an son dernier coef
posons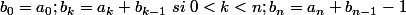 . Alors
En binaire c'est encore plus simple puisqu'il suffit de mettre 1 dans chaque position indiquée par les bi et de compléter par des zéros
exemple 65/17 donne la suite des a : (3,1,4,1,2) et des b : (3,4,8,9,10)
donc x=11100011000 (on a mis des 1 en 3ième, 4ième ...10ième position à compter de la droite, la position zéro est celle des unités)
1 démarche avec une suite double pour ceux qui sont allergiques aux fractions continues (ils ont tort :zen: )
Soit y=p/q et les suites

Ces suites sont finies et l'on s'arrête quand un=1.
Il faut ôter 1 au dernier b et la suite bn se décode en décimal ou binaire comme ci dessus (sauf qu'ici on démarre de 1 et non de zéro)
Les deux méthodes sont, bien entendu strictement équivalentes et très faciles à programmer

EDIT je viens de voir ton message Imod, effectivement j'ai l'impression qu'on est proches mais il est trop tard et les histoires de familles m'ont toujours épuisé... je lirais demain tranquillement les aventures du frère du père (et en plus il ya des ainés et des cadets !) :dodo:

[pedro_cristian]

Non non c'est bien une bijection de N
Je l'inverse de manière un peu différente de Zebulon (ent=partie entière) :
et x=n-y
Bien sur, ça doit revenir au même mais c'est plus facile à programmer :we:

J'espere que je ne suis pas trop H.S., mais dans le genre bijection simple (je crois que je ne l'ai pas vu passer), il y a bien qui définit une bijection de |N^2 ver |N puisque tout nombre plus grand que 1 est une puissance de 2 multiplié par un nombre impair. Ce qui donne avec les compositions adéquates toutes les bijections de |N^n vers N.

[alben]

Bonsoir,
Oui, elle n'est pas très éloignée de celle de yos et pas trop difficile à inverser.
En fait, je crois qu'à l'origine, c'était une bijection dont la fonction réciproque ne sois pas facile à déterminer qui était recherchée.

[pedro_cristian]

Ces interventions avec toute leur complexité me rappellent l'éblouissement que j'ai eu quand j'ai découvert la théorie des cardinaux et ordinaux "les bijections existent" mais de là à les expliciter ... Q en bijection avec N !!!!
Un gros coup de chapeau à Cantor .

Imod

Je trouve que la bijection entre les nombre rééls non transcendants et N est plus impressionnante. (j'espère que je ne dis pas de connerie..)

[Imod]

Je trouve que la bijection entre les nombre rééls non transcendants et N est plus impressionnante. (j'espère que je ne dis pas de connerie..)

Oui ( non trancendants = algébriques :we: ) , mais je crois que lorsqu'on a réussi à digérer que N et Q sont équipotents , on est pret pour admettre que N est en bijection avec l'ensemble des nombres algébriques et pour bien d'autres choses .

Imod

[alben]

Bonjour,
Je n'ai pas le souvenir d'une bijection explicite entre les algébriques et N.
As-tu ça pedro_cristian ?

[pedro_cristian]

Bonjour,
Je n'ai pas le souvenir d'une bijection explicite entre les algébriques et N.
As-tu ça pedro_cristian ?

Non non, je n'ai pas le souvenir d'une bijection explicite.

[yos]

Les algébriques sont en bijection avec les polynômes minimaux à coef entiers dont ils sont racines. Il suffit donc de ranger convenablement ces polynômes.
On peut prendre les polynomes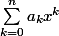 qui vérifient 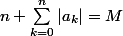. Ils forment un ensemble fini 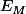. Et l'ensemble de ces polynômes est la réunion des 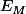, pour M décrivant .
Une réunion dénombrable d'ensembles finis est finie.
Après, cela dépend ce qu'on appelle explicite. Ce qui précède l'est dans la mesure où il est facile d'ordonner chaque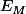 . Vouloir une "formule" me semble un peu vain.

[oss007]

Bonjour,
dans l'exemple de zébulon, 7 et 141 , par exemple, n'ont pas d'antécédents.

[alben]

Les algébriques sont en bijection avec les polynômes minimaux à coef entiers dont ils sont racines. Il suffit donc de ranger convenablement ces polynômes.
On peut prendre les polynomes qui vérifient . Ils forment un ensemble fini . Et l'ensemble de ces polynômes est la réunion des , pour M décrivant .
Une réunion dénombrable d'ensembles finis est finie.
Après, cela dépend ce qu'on appelle explicite. Ce qui précède l'est dans la mesure où il est facile d'ordonner chaque . Vouloir une "formule" me semble un peu vain.

Oui le fait que les algébriques soient dénombrables n'est pas très difficile à démontrer sachant qu'une réunion dénombrable d'ensembles finis ou dénombrables est dénombrable (qui résulte directement du fait que N² est en bijection avec N).
D'accord aussi sur la vanité de la démarche consistant à expliciter la bijection.
Mais est-ce plus vain que la recherche de la sempiternelle convergence d'une série truffée de log et de racines ? :we:
Un point de détail :
Il me semble que les algébriques ne sont pas vraiment en bijection avec les polynomes minimaux à coef entiers, deux algébriques peuvent partager le même polynome minimal.
Ce n'est pas vraiment un argument car il suffit de prendre des coeff premiers entre eux pour la racine la plus faible et ensuite de multiplier par les nombres premiers successifs.
On peut facilement construire une injection dans N avec une technique similaire à celle de la fonction d'Imod

[Imod]

Voilà une démo qui me semble à peu près exhaustive et qui n'est pas très lourde.

Une fois toutes les idées posées , on peut faire bien plus court ( garanti sans histoires de famille ) . . Si A est non vide , on peut choisir dans A avec p minimal pour q minimal , nécessairement p>q . En posant et p'=p-kq alors ce qui est impossible car p'<p .
En effet si et alors .

Imod

[alben]

[quote="Imod"]Une fois toutes les idées posées , on peut faire bien plus court ( garanti sans histoires de famille ) . . Si A est non vide , on peut choisir dans A avec p minimal pour q minimal , nécessairement p>q . En posant et p'=p-kq alors ce qui est impossible car p' à q

[Imod]

Oui, j'avais vu qu'on n'était pas obligé de se limiter à ]0;1[. En revanche, construire A directement comme partie de Q et non de N me gêne. Je n'ai pas compris pourquoi p est nécessairement > à q

p>q sinon car et sont simultanément dans A ou hors de A . Je vois bien aussi en quoi te gène le fait de choisir une partie de Q car rien ne garantit l'existence d'un plus petit élément c'est pour çà que je pris soin de prendre q ( entier ) minimal et parmi les avec ce q fixé , p ( entier ) minimal .

Imod

[alben]

D'accord pour l'existence de l'élément doublement mini comme tu viens de le définir.
En revanche je ne comprends toujours pas p>q d'autant que p est le mini. En outre je ne pense pas que tu en ais besoin.
si p>q on arrive à p'

si pdans les deux cas contradiction.

[Imod]

D'accord il y a contradiction dans les deux cas mais c'est parce que je n'avais pas envie d'étudier les deux cas que je précisais que p>q . Je détaille un peu . . Si n est pair et si n est impair donc 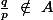. Alors 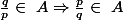. Si p était plus petit que q , en échangeant le numérateur et le dénominateur on contredirait le choix de q .

Imod