Un entier

[Lutinette18]

Bonsoir!

je n'ai pas tout à fait abouti à l'exercice suivant :

il s'agit de montrer que pour tout n entier,
(5*n)! / (40^n)*(n!) est entier.

J'ai procédé par récurrence. Je veux montrer la propriété pour n+1. En utilisant l'hypothèse de récurrence, je tombe finalement sur : (5n+1)(5n+2)(5n+3)(5n+4)/8
Je pense donc que je m'y suis mal prise...

Merci pour vos idées!! :we:

[leon1789]

je tombe finalement sur : (5n+1)(5n+2)(5n+3)(5n+4)/8

Si cela peut te rassurer, effectivement, le produit de 4 entiers consécutifs est toujours multiple de .

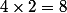
[Lutinette18]

j'ai essayer de voir pour n=600 et cette propriété n'est pas vérifiée.
Petit problème!

[leon1789]

j'ai essayer de voir pour n=600 et cette propriété n'est pas vérifiée.

602 est divisible par 2 et 604 divise par 4, donc 602*604* est divisible par 8.
...et je t'assure que est entier.

De quelle propriété parles-tu ?

[Lutinette18]

je veux dire que j'ai calculé : (5*600+1)* ....*(5*600+4) et que ce nombre n'est pas divisible par 8 d'après ma petite calculette.
J'ai peut être mal compris ce que tu veux dire?

[leon1789]

je veux dire que j'ai calculé : (5*600+1)* ....*(5*600+4) et que ce nombre n'est pas divisible par 8 d'après ma petite calculette.

Et bien voilà un bel exemple où se fier à sa calculette est une mauvaise chose :zen:

5*600 + 2 est divisible par 2
5*600 + 4 est divisible par 4
donc (5*600+1)*(5*600+2)*(5*600+3)*(5*600+4) est divisible par 2x4=8 !

Regarde, le principe est évident !

[leon1789]

je veux dire que j'ai calculé : (5*600+1)* ....*(5*600+4) et que ce nombre n'est pas divisible par 8 d'après ma petite calculette.

Comment expliques-tu le fait que ta calculette se trompe ? (question sérieuse)

[Lutinette18]

Elle trouve : 1.015....

[leon1789]

Elle trouve : 1.015....

bon ok, elle trouve ça... après quel calcul ?

[Lutinette18]

après celui là (5*600+1)*(5*600+2)*(5*600+3)*(5*600+4)/8

[leon1789]

Et après 8*1.015, elle donne quoi ta calculette ?

[Doraki]

c'est 10158789393753, soit environ 1.015 *10^13, ce que la calculatrice essaie de te dire parcequ'elle peut pas afficher suffisemment de chiffres pour afficher ce nombre en entier.

[leon1789]

c'est 10158789393753, soit environ 1.015 *10^13, ce que la calculatrice essaie de te dire parcequ'elle peut pas afficher suffisemment de chiffres pour afficher ce nombre en entier.

tu n'aurais pas dû le dire...

[Lutinette18]

ah :D heureusement que vous êtes là!!!

merci beaucoup

[Doraki]

C'est vrai que ne pas se dire qu'il y a un problème quand on voit la calculatrice dire 3001*3002*3003*3004/8 = 1.015 sachant que 8*1.015 n'est même pas entier, c'est fort.
Et douter du résultat à montrer plutôt que de la calculatrice après un truc aussi invraisemblable ?

[leon1789]

oh oui !
Et en plus :
Forum mathématique > Questions/réponses scolaires > Supérieur

[Lutinette18]

oui, je suis encore jeune :help: mais je tire des leçons :++:

[leon1789]

oui, je suis encore jeune :help: mais je tire des leçons :++:

Il serait temps : lire sur une calculatrice, ça se fait bien avant le supérieur je crois.