Ensembles mesurables.
19 messages
- Page 1 sur 1
Ensembles mesurables.
Bonjour, voici l'énoncé de mon exercice : Soit (oméga, B, u) un espace mesuré avec u(oméga) = 1. Soit également (fn) une suite de fonctions mesurables sur oméga, à valeurs réelles. On suppose que la suite (fn) converge simplement vers une fonction f. Dans toute la suite, on fixe epsilon > 0.
1) Soit k appartenant à N étoile. Pour n appartenant à N, on pose :
An = {x appartenant à oméga; pour tout p >=n : valeur absolue (fp(x) - f(x)) < 1/k}.
Justifier que les An sont mesurables.
Mon problème est que je ne sais pas ce que je dois montrer en fait...
Merci
1) Soit k appartenant à N étoile. Pour n appartenant à N, on pose :
An = {x appartenant à oméga; pour tout p >=n : valeur absolue (fp(x) - f(x)) < 1/k}.
Justifier que les An sont mesurables.
Mon problème est que je ne sais pas ce que je dois montrer en fait...
Merci
Re: Ensembles mesurables.
Salut,
A mon avis, ce que tu doit montrer, c'est que... tout les An sont mesurables...
Ensuite, si "tu ne sait pas ce qu'il faut montrer", ça peut aussi venir du fait que tu sait pas ce que veut dire qu'une partie de est mesurable ou bien qu'il y a d'autre expression de l'énoncé dont tu ne sais pas ce que ça veut dire.
est mesurable ou bien qu'il y a d'autre expression de l'énoncé dont tu ne sais pas ce que ça veut dire.
Bref, la première chose à faire, c'est bien évidement de chercher les définitions de
- espace mesuré
- fonction mesurable
- convergence simple (mais c'est pas utile pour le moment)
- ensemble mesurable
Et avec ça plus epsilon (=petit théorème concernant les fonctions mesurables), tu as ta réponse.
A mon avis, ce que tu doit montrer, c'est que... tout les An sont mesurables...
Ensuite, si "tu ne sait pas ce qu'il faut montrer", ça peut aussi venir du fait que tu sait pas ce que veut dire qu'une partie de
Bref, la première chose à faire, c'est bien évidement de chercher les définitions de
- espace mesuré
- fonction mesurable
- convergence simple (mais c'est pas utile pour le moment)
- ensemble mesurable
Et avec ça plus epsilon (=petit théorème concernant les fonctions mesurables), tu as ta réponse.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
PS : n dépend de k
An est une partie de Ω où |fn-f|<1/k
je pense qu'on va ensuite te demander de prouver que An+1 ⊂ An
et que si la limite est d'intérieur non vide, en restreignant fn à la limite des Ap, tu as une convergence uniforme.
et derrière une réciproque ?
An est une partie de Ω où |fn-f|<1/k
je pense qu'on va ensuite te demander de prouver que An+1 ⊂ An
et que si la limite est d'intérieur non vide, en restreignant fn à la limite des Ap, tu as une convergence uniforme.
et derrière une réciproque ?
Re: Ensembles mesurables.
Je comprend pas ce que tu veut dire avec ton "n dépend de k".pascal16 a écrit:PS : n dépend de k
An est une partie de Ω où |fn-f|<1/k
Et An, de savoir uniquement que c'est UNE partie où |fn-f|<1/k, ça va pas suffire pour montrer que An est mesurable (vu que ça te donne juste une inclusion).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
En fait, je ne sais pas ce que signifie qu'une partie est mesurable. Donc forcément, j'ai aucune idée de ce que je dois faire...
Re: Ensembles mesurables.
Et un espace mesuré ) , tu sait ce que c'est ?
, tu sait ce que c'est ?
Si oui, ben ça veut dire que tu sait ce qu'est une "partie mesurable" : c'est simplement un élément de la tribu (*).
(*).
Si non, ben je vois pas bien ce que tu fait à te lancer dans un tel exo...
(*) Ou éventuellement un élément de la tribu complétée, mais on va pas rentrer dans les "finasseries"...
Si oui, ben ça veut dire que tu sait ce qu'est une "partie mesurable" : c'est simplement un élément de la tribu
Si non, ben je vois pas bien ce que tu fait à te lancer dans un tel exo...
(*) Ou éventuellement un élément de la tribu complétée, mais on va pas rentrer dans les "finasseries"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
J'ai dit que An est l'image réciproque par fp-f de [0, 1/k]. Puisque fp-f est mesurable alors A est mesurable car l'image réciproque de tout intervalle est mesurable. Est ce bien cela?
Re: Ensembles mesurables.
Non : y'a (un peu) de l'idée, mais il manque un paquet de trucs :lightone a écrit:J'ai dit que An est l'image réciproque par fp-f de [0, 1/k]. Puisque fp-f est mesurable alors A est mesurable car l'image réciproque de tout intervalle est mesurable. Est ce bien cela?
- Déjà, c'est pas fp-f, mais |fp-f|.
- Vu que l'énoncé dit uniquement que les fp sont mesurables, il faudrait évidement expliquer pourquoi la fonction |fp-f| l'est aussi (si tant est que c'est vrai...)
- An c'est pas l'image réciproque de [0,1/k] par |fp-f| (si c'était ça, ben ça dépendrait pas de n mais uniquement de p et k)
Tu as fait quoi du "pour tout p>=n" qu'il y a dans la définition de An ? (poubelle ?)
Modifié en dernier par Ben314 le 29 Sep 2018, 18:17, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
- Ba vu que les fn sont mesurables, valeur absolue de fp-f est mesurable car c'est l'addition de 2 fonctions mesurables?
- Ah je ne sais pas par contre pour ça...
- Ah je ne sais pas par contre pour ça...
Re: Ensembles mesurables.
Ha bon ?lightone a écrit:- Ba vu que les fn sont mesurables, valeur absolue de fp-f est mesurable car c'est l'addition de 2 fonctions mesurables ?
Y'a marqué que f est mesurable dans l'énoncé ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
Ba non mais le f est forcément mesurable puisqu'il correspond à un fn quand n tend vers l'infini. Donc il fait partie aussi de (fn) pour moi.
Re: Ensembles mesurables.
Attention ! L'infini n'est pas un nombre ! Donc  est une suite de fonctions, un terme pour chaque entier naturel
est une suite de fonctions, un terme pour chaque entier naturel  , mais qui ne contient pas
, mais qui ne contient pas  !
!
Voici un contre-exemple dans un autre cas : soit sur [0;1]. Toutes les
sur [0;1]. Toutes les 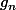 sont continues.
sont continues.
Mais que dire de , limite simple des
, limite simple des 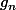 ?
? =0) sur
sur 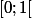 et
et =1) ,
,  n'est donc pas continue.
n'est donc pas continue.
C'est donc un contre-exemple où une suite de fonctions a une propriété, mais sa limite simple ne l'a pas...
Pour en revenir à) et à
et à  : peut-on dire que la limite simple d'une suite de fonctions mesurables est mesurable ?
: peut-on dire que la limite simple d'une suite de fonctions mesurables est mesurable ?
Voici un contre-exemple dans un autre cas : soit
Mais que dire de
C'est donc un contre-exemple où une suite de fonctions a une propriété, mais sa limite simple ne l'a pas...
Pour en revenir à
Modifié en dernier par hdci le 29 Sep 2018, 18:31, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Ensembles mesurables.
Et si je t'écrit la même chose avec par exemple "continue" à la place de "mesurable", c'est à dire (en supposant bien sûr que les fn sont continus) :lightone a écrit:Ba non mais le f est forcément mesurable puisqu'il correspond à un fn quand n tend vers l'infini. Donc il fait partie aussi de (fn) pour moi.
Ba non mais le f est forcément continue puisqu'il correspond à un fn quand n tend vers l'infini. Donc il fait partie aussi de (fn) pour moi.
Tu en pense quoi comme raisonnement ?
Et celui là (en supposant que tout les réels Un sont strictement positifs et que la suite Un tend vers L) :
Ba non mais le L est forcément strictement positif puisqu'il correspond à un Un quand n tend vers l'infini. Donc il fait partie aussi de (Un) pour moi.
Idem avec une suite de rationnels qui tend vers L : tu en déduit que L est rationnel ?
Modifié en dernier par Ben314 le 29 Sep 2018, 18:32, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
Recherche donc dans ton cours à quelle condition la limite simple d'une suite de fonctions mesurable est mesurable.
Tu dois avoir cela assez près des bornes supérieures, bornes inférieures, limite supérieure et limite inférieure.
Tu dois avoir cela assez près des bornes supérieures, bornes inférieures, limite supérieure et limite inférieure.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Ensembles mesurables.
J'ai un corollaire qui me dit que si (fn) est une suite de fonctions qui converge vers f alors f est mesurable. Sauf que ce fn va de oméga dans R barre.
Re: Ensembles mesurables.
Ben p'têt bien que justement il faudrait se poser la question de savoir si, lorsqu'une suite (fn) de fonctions mesurable de  dans
dans  converge vers une certaine fonction
converge vers une certaine fonction  , est ce que forcément la fonction
, est ce que forcément la fonction  est mesurable ?
est mesurable ?
Et là où ça me "trou le cul", c'est de voir qu'on peut en être au point d'étudier les espaces mesurés alors qu'on à même pas compris que tout les truc du style "si tout les termes d'une suite sont XXX alors la limite est elle même XXX", ben y'en a des tonnes qui sont archi faux et que quand c'est vrai, c'est absolument jamais "une évidence", mais systématiquement un truc qu'on démontre (et c'est parfois assez difficile)
Et là où ça me "trou le cul", c'est de voir qu'on peut en être au point d'étudier les espaces mesurés alors qu'on à même pas compris que tout les truc du style "si tout les termes d'une suite sont XXX alors la limite est elle même XXX", ben y'en a des tonnes qui sont archi faux et que quand c'est vrai, c'est absolument jamais "une évidence", mais systématiquement un truc qu'on démontre (et c'est parfois assez difficile)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Ensembles mesurables.
Oui ba écoutez, c'est une matière où l'on a pas de TD et les seuls exos que l'on a, sont des DM à rendre chaque semaine et qui sont notés. On fait ce que l'on peut pour essayer de résoudre nos exercices.
Re: Ensembles mesurables.
lightone a écrit:J'ai un corollaire qui me dit que si (fn) est une suite de fonctions qui converge vers f alors f est mesurable. Sauf que ce fn va de oméga dans R barre.
OK, donc ton cours te donne une piste.
Que peut-on dire de
Du coup, peut-on dire d'une fonction de
Question subsidiaire : et si la fonction est de
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

