Ensembles denses

[ludo56]

Bonjour, je n'arrive pas a comprendre un passage dans un bouquin alors je solicite votre aide :

Soit L une partie de H un Hilbert . Il est ecrit que puisque L n'est pas dense dans H il existe donc un element x non nul de H tel que =0 pour tout y de L . La seule definition que je connais est : puisque L non dense dans H alors il existe x dans H tel que x n'est pas limite d'eléments de L et je ne vois pas le lien avec ce qui est ennoncé.
Merci d'avance!

[ThSQ]

Prends le sous-espace E engendré par L.
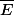
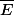
Par combinaison linéaire tout orthogonal à L est orthogonal E et par limite à . est donc un sev fermé strict + théorème de projection classique.

[Maxmau]

Bonjour, je n'arrive pas a comprendre un passage dans un bouquin alors je solicite votre aide :

Soit L une partie de H un Hilbert . Il est ecrit que puisque L n'est pas dense dans H il existe donc un element x non nul de H tel que =0 pour tout y de L . La seule definition que je connais est : puisque L non dense dans H alors il existe x dans H tel que x n'est pas limite d'eléments de L et je ne vois pas le lien avec ce qui est ennoncé.
Merci d'avance!

Bj
suis perplexe
pourtant il existe des parties de R² non denses dans R² et non contenues dans une droite. ??? L partie ou SEV de H ???

[Joker62]

Mais s'bien on a l'équivalence entre L dense et L orthogonal est réduit à {0}
Ici L n'est pas dense, donc L ortho n'est pas nul, il existe donc bien un élément dans L ortho c'est à dire un élément de H orthogonal à tout élément de L :^)

Enfin dans le cas où L est un sev
Si c'est une partie on le fait à la sauce TéHacheSciu

[yos]

J'appuie Maxmau. Si L est une partie génératrice de H, ça foire.

[ThSQ]

J'appuie yos, l'auteur du post #2 est un crétin !

[Joker62]

Rassurez les crétins qui suivent les crétins svp !!!
Quand L sev c'est ok ? :D

[ThSQ]

Dans le cas d'un sev non dense, je dirais oui.

Sinon deux vecteurs non colinéaires dans R² fournissent un contrex assez humiliant :ptdr:

[yos]

Bah la vraie force, c'est de réussir à prouver n'importe quoi (y compris des choses fausses) puis de trouver des disciples qui confirment.
L'initiateur de la question ne se souvient plus qu'il l'a posée (comme souvent). Je soupçonne un logiciel qui génère des questions. Genre big brother keeping you busy.

[ThSQ]

Je vais créer une nouvelle religion ou un nouveau partie politique !