Ensembles dénombrables

[minidiane]

Bonjour je n'arrive pas à démontrer que l'intervalle des nombres réels [0,1] n'est pas dénombrable et à montrer que {0,1}^N :={(x_i)i appartenant à N: x_i appartenant à {0,1}} n'est pas dénombrable. Indication donnée:(Montrer que si D inclu dans {0,1 =^N est dénombrable alors on peut construire une nouvelle suite (x^i)_(i appartenant à N) appartient ç {0,1}^N en dehors de D!)
Pouvez-vous m'aidez svp
Merci

[Joker62]

On suppose qu'il est dénombrable,
On le découpe en trois
Alors il existe forcément un élement de la suite qui n'appartient pas à un des 3 intervalles créer.
On recommence avec l'intervalle dans lequel on a choisi l'élément
On le découpe en trois... etc... etc...

On va arriver à une contradiction

[minidiane]

Il faut faire cela pour les deux démonstrations?

[Joker62]

Non ça c'est pour montrer que [0;1] n'est pas dénombrable.

[Joker62]

Pour la deux, ça sent la décomposition diadique de Cantor.
Va voir du côté de l'argument de la Diagonale de Cantor

[minidiane]

oula je ne connais pas du tout je vais voir si je trouve quelque chose sur google ;)

[legeniedesalpages]

Bonjour, oui l'indication indique clairement qu'il faut utiliser la diagonale de Cantor, sinon on peut montrer que est en bijection avec , et conclure à l'aide du théorème de Cantor.

[minidiane]

ok est-ce que quelqu'un peut me donner la définition de la diagonale de Cantor et son théorème? car je ne comprend pas trop ce que j'ai trouvé sur le net
merci

[fahr451]

bonjour

voila le procédé diagonal de cantor

on suppose qu'on peut dénombre les suites dont les termes valent 0 ou 1

on en fait donc une numération soit

(x^(n) )ndans N une telle numérotation on a donc toutes les telles suites

x^(0) , x^(1) etc ... sont donc des suites

on écrit

x^(0) = (x^(0) 0 ,x^(0) 1,..)
x^(0) 0 est le premier terme de la suite x^(0)

on construit une suite x telle que x0 soit différent de x^(0) 0

si x^(0) 0 = 1 on prend 0 et inversement
la suite x est donc différent de la suite x^(0)
on impose aussi que

x1 différent de x^(1) 1

la suite x est différente de la suite x^(1)

d'une façon générale on impose

pour tout n
xn différent de x^(n) n

donc la suite x est différente de toutes les suites x^(n)

et pourtant est bien une suite de termes 0 ou1

on avait supposé qu'on les avait toutes avec les x^(n)
c'est absurde

[minidiane]

ok merci fahr je crois que j'ai compris le procédé, par contre pour l'appliquer c'est encore autre chose.

[Joker62]

Il suffit de dire : par le procédé de la diagonale de Cantor, on extrait un élément etc...

[juve1897]

Bonjour,

desolée de m'incruster dans ce topic, mais je suis aussi sur un exercice sur les ensembles dénombrables.

En fait la definition nous est énoncée et on nous demande de verifer que qq ensembles sont denombrables.

MAis je ne vois vraiment pas comment proceder à la demonstration.

Est ce que qqun pourrait m'eclairer un peu ?

Merci bcp :happy2:

[Joker62]

Un ensemble E est dénombrable si on peut le mettre en bijection avec N

Le but est donc de construire une bijection.
Montre sur quoi tu bloques.

[juve1897]

Un ensemble E est dénombrable si on peut le mettre en bijection avec N

Le but est donc de construire une bijection.
Montre sur quoi tu bloques.

Ben c'est sur la definition que je bloque, je comprends qu'il y'a une histoire de bijection mais le reste ???

en fait je dois montrer que des ensembles tel que Z, les entiers impairs .

En par la suite je dois verifier que
1) l'union de 2 ensemble dénombrables est dénombrable (en supp que les 2 sont disjoint)

2) un sous ensemble infini d'un ensemble infini denombrable est infini denombrable

Mais j'aimerai simplement que l'on m'explique comment faire dans un cas general.

Merci Joker

[Joker62]

Pour montrer que Z est dénombrable :

On cherche une application g de Z dans N tel que g soit bijective

On pose

g(z) = 2z si z € N
g(z) = -(2z+1) si z € Z\N

g(0) = 0
g(-1) = 1
g(1) = 2
g(-2) = 3
g(2) = 4
g(-3) = 5

...
Tu vérifies qu'elle est bijective et voilà Z est dénombrable
On peut compter les entiers relatifs.

[juve1897]

Pour montrer que Z est dénombrable :

On cherche une application g de Z dans N tel que g soit bijective

On pose

g(z) = 2z si z € N
g(z) = -(2z+1) si z € Z\N

g(0) = 0
g(-1) = 1
g(1) = 2
g(-2) = 3
g(2) = 4
g(-3) = 5

...
Tu vérifies qu'elle est bijective et voilà Z est dénombrable
On peut compter les entiers relatifs.

Merci joker, j'ai vu cette demo sur Wikipedia, mais je ne comprends pas ...
je ne vois pas quand je dois faire intervenir Z et N. :marteau:

PEux tu m'expliquer comment on procede en general ? Car tu mets arbitrairement
g(z) = 2z si z € N
g(z) = -(2z+1) si z € Z\N

mais comment tu trouves les "g(z)" ?

Merci.

[legeniedesalpages]

Bonjour,

tu prends un entier relatif z, à l'aide de cette fonction, si il est positif tu l'envoies vers un entier naturel pair, si il est strictement négatif tu l'envoies vers un entier naturel impair.

Il n'y a pas de cas général, c'est juste intuitif.

tu peux aussi montrer que - est dénombrable, puis 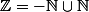est une union dénombrable en tant qu'union de deux ensembles dénombrables.

[juve1897]

Bonjour,

tu prends un entier relatif z, à l'aide de cette fonction, si il est positif tu l'envoies vers un entier naturel pair, si il est strictement négatif tu l'envoies vers un entier naturel impair.

Il n'y a pas de cas général, c'est juste intuitif.

tu peux aussi montrer que - est dénombrable, puis est une union dénombrable en tant qu'union de deux ensembles dénombrables.

MErci pour ta reponse.

Je vais d'abord essayé de comprendre la definition, car je crois que c'est à ce niveau la que ça coince le plus

[legeniedesalpages]

quelle définition?

[juve1897]

quelle définition?

la definition d'un ensemble denombrable:

Un ensemble infini E est denombrable s'il existe une bijection de E vers N
soit card(E) = card(N)

Je n'arrive pas vraiment à la comprendre/