Ensemble mesurable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 28 Sep 2014, 17:19
par joanie58 » 28 Sep 2014, 17:19
Bonjour,
est-ce qu'il est possible de construire, pour tout

, un ensemble mesurable non borné dans

dont la mesure de Lebesgue est égale à

.
Merci
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 28 Sep 2014, 17:35
par jlb » 28 Sep 2014, 17:35
joanie58 a écrit:Bonjour,
est-ce qu'il est possible de construire, pour tout

, un ensemble mesurable non borné dans

dont la mesure de Lebesgue est égale à

.
Merci
A vérifier, mais en adjoignant à un bon hyper cube un bon ensemble de mesure nul cela doit être possible, non?
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 28 Sep 2014, 17:56
par joanie58 » 28 Sep 2014, 17:56
je ne comprend pas se que vous voulez dire par en adjoignant à un bon hyper cube... qu'est-ce qu'un hyper cube
-
mathelot
 par mathelot » 29 Sep 2014, 05:00
par mathelot » 29 Sep 2014, 05:00
joanie58 a écrit:je ne comprend pas se que vous voulez dire par en adjoignant à un bon hyper cube... qu'est-ce qu'un hyper cube
c'est le produit cartésien de n segments (un cube).
tu prend un (hyper)cube de largeur
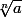
réuni avec
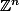
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 05 Oct 2014, 19:12
par joanie58 » 05 Oct 2014, 19:12
mathelot a écrit:c'est le produit cartésien de n segments (un cube).
tu prend un (hyper)cube de largeur
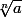
réuni avec
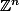
Est-ce que cet ensemble fonctionne:
=\sqrt[n]{a}})
-
joanie58
- Membre Relatif
- Messages: 115
- Enregistré le: 04 Fév 2013, 21:17
-
 par joanie58 » 05 Oct 2014, 19:28
par joanie58 » 05 Oct 2014, 19:28
je ne voit pas le lien entre mes deux questions
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
, un ensemble mesurable non borné dans
dont la mesure de Lebesgue est égale à
.