Ensemble de définition du logarithme

[freddywill]

Bonjour, je me présente, je suis étudiant en 2ème année de licence de Maths-Physique à la faculté d' Orsay (qui par ailleurs est une excellente faculté) et depuis peu j'essaie de répondre à des questions fondamentales dont j'avais admis la réponse au lycée telles que :

Pourquoi le logarithme n'est-il définie que sur ]o;+;)[ ?

De fait cela paraît évident lorsqu'on considère le logarithme en temps que la primitive de x;)1/x ou bien la réciproque de l'exponentielle.

Mais si on le considère - et c'est la ma véritable question - en temps que la fonction vérifiant la propriété
log(ab) = log(a) + log(b) (1)
Alors je ne comprends pas pourquoi elle ne pourrait pas être définie sur les réels négatifs (l'asymptote en 0 allant de soi).

Soient a,b deux réels positifs, je ne comprends pas pourquoi on ne pourrait pas écrire :
log(-ab) = log(-a) + log(b)
= log(a) + log(-b)

Je précise que (1) est la première définition du logarithme, celle de Neper, ce qui n'est donc pas celle que l'on apprend au lycée.

[windows7]

salut

recherche sur google " logarithme complexe "

[Nightmare]

Salut !

En fait, rien n'empêche de définir un logarithme sur ]-oo;0[ puisque x->1/x admet des primitives sur cet intervalle... La question est de savoir si ça a une utilité de le faire, en particulier, savoir si on a de belles propriétés comme sur ]0;+oo[ ...

[busard_des_roseaux]

bonjour,

déja sur R*-, on peut écrire

ln(ab)=ln(-a)+ln(-b)



ensuite ,effectivement , on définit un logarithme complexe
c'est toute fonction holomorphe f, définie sur un ouvert connexe de 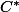, non vide qui vérifie



on cherchant une telle fonction, on s'aperçoit que nécessairement
l'ouvert ne doit pas contenir de lacet (chemin continu fermé de même origine et extrémité )
entourant l'origine.

On dit que doit être simplement connexe

Quand l'ouvert est simplement connexe, alors
l'angle polaire de la variable z est définie de
manière univoque, comme fonction de z, et donne un logarithme par la formule



en effet



déja , localement, comme les coordonnées polaires
donnent



modulo

on différentie ce machin là




L'intégrale de cette forme différentielle sur tout chemin de à donne un argument polaire de dont la définition
ne dépend pas de


où est un chemin quelconque allant de à z ,chemin n'entourant pas l'origine O.

[Doraki]

On peut faire ça et d'ailleurs le seul moyen simple est de décider que log(-x) = log(x). Parceque 2 * log(-1) = 0, et jusqu'à nouvel ordre, dans les nombres, y'a que 0 qui donne 0 quand on l'additionne avec lui-même.

La propriété de log(ab) = log(a) + log(b) reste vérifiée.

L'ennui c'est que ça n'apporte rien aux autres propriétés :
log n'est plus injectif, donc plus inversible.
Y'a un bout de la fonction qui est "la primitive de 1/x qui vaut 0 en 1", et l'autre bout qui est "la primitive de 1/x qui vaut 0 en -1", et y'en a pas un qui serait un prolongement naturel de l'autre (être une primitive de quelquechose est une propriété locale, ce qui peut faire des problème après, quand on regarde le log sur C)

[busard_des_roseaux]

On peut faire ça et d'ailleurs le seul moyen simple est de décider que log(-x) = log(x)

à mon avis, le plus naturel est de couper le plan complexe
selon (les imaginaires négatifs ou nuls)
et de définir par exemple


ce qui donne



déja , sans faire "varier" quoique ce soit, si on pose
u=a+ib=log(z)
alors

on voit donc que doit être une écriture trigonométrique de z, ce qui donne pour a

a=ln(|z|)=ln(r)
b= un argument (ou angle polaire) de z.

on est donc conduit à poser nécessairement


le souci, c'est que cesse d'être une fonction
si on fait un tour autour de l'origine O

[Doraki]

Bah au début il ne parlait pas de complexes alors j'ai évité le sujet.

J'aime pas dire "on peut définir log comme étant la primitive de 1/z qui vaut 0 en 1 sur les ensembles simplement connexes qui ne contiennent pas 0",
parceque c'est pas "simplement connexe" qu'est important, c'est "qui ne contienne pas de lacet autour de 0".

La fonction log (ou toute autre fonction définie comme étant une primitive) ne s'applique pas à une valeur, mais à un chemin :
Je préfère dire carrément "on peut définir log comme étant la primitive de 1/z qui vaut 0 en 1 sur le revêtement universel de C*" (ou bien l'ensemble des chemins de C* partant de 1, quotienté par l'homotopie), parce que ça explique mieux ce que c'est qu'une primitive.

Ca permet de dire "il existe un chemin de 1 à -1 qui donne log(-1) = ipi" (et qu'il y a aussi des chemins qui donnent log(-1) = (2k+1)pi),
ça garde la propriété log(a*b) = log(a) + log(b), en expliquant que le "produit" d'un chemin f qui va de 1 à a, et d'un chemin g qui va de 1 à b, est le chemin fg(t) = f(t)*g(t), qui va de 1 à a*b.

Et enfin, log reste une bijection entre C et le revêtement universel de C*,
et si on fait la composée de sa réciproque avec la projection canonique du revêtement universel de C* sur C*, ça redonne exactement la fonction exponentielle comme on la connaît.
Autrement dit, que la fonction exponentielle et la projection du revêtement universel de C* sur C*, c'est à peu près la même chose.

[busard_des_roseaux]

ça garde la propriété log(a*b) = log(a) + log(b), en expliquant que le "produit" d'un chemin f qui va de 1 à a, et d'un chemin g qui va de 1 à b, est le chemin fg(t) = f(t)*g(t), qui va de 1 à a*b.

le souci, me semble t il , comme arg(ab)=arg(a)+arg(b)
faut pas que la somme fasse plus d'un tour sinon il n' y a plus l'équivalence
homotopique. faut regarder dans le détail, mais le problème du log, c'est que les angles polaires ne sont pas définis du tout modulo mais effectivement en suivant des chemins du plan complexe.

[vingtdieux]

log(ab) ne definit par une fonction car c'est a partir de deux variables a et b. On arrive bien a log1=0 en posant b=1, et apres? loga=loga. That's all...
Alors c'est vrai que si on étend aux complexes c'est autre chose. Et le log neperien est:
Lnz=Ln|z|+iArgz
Ainsi Ln(-1)=iPi (peace and love) :zen: