Ensemble algebrique

[Doraki]

Peut-être mais en géométrie algébrique, une droite affine c'est Spm k[X].
(ou spec si tu fais des schémas)

[barbu23]

oui, mais je comprends pas pourquoi ! :happy3:

[barbu23]

Bonsoir : :happy3:
Je n'apprends pas en ce moment la geometrie al gebrique ni je connais beaucoup de choses de cette discipline , mais je voudrais que vous m'aidiez sur certains points interessants pour comprendre bien la geometrie differentielle : parmi ces points, la notion de faisceau :
Par definition , un faisceau et un prefaiceau qui verifient les conditions de recollements suivant s :
- Soit un ouvert et un recouvrement d'ouverts de ,alors :
:
- tel que : , il existe : tel que pour tout : .
Pourquoi celà equivaut à dire que la suite courte suivante est exacte :

où la prmière flèche est : , la deuxième est :

[barbu23]

pour la première flèche, , c'est clair, pourquoi, c'est injective, d'après la première assertion des deux conditions de recollements : : ! :happy3:

[Finrod]

Ta question m'embêtes un peu.

Je pense qu'il faut cherhcer la réponse dans l'orignie de théorie des schémas. C'est ce qui a motivé la théorie qui permet de comprende le lien ente le spectre de ces anneaus et des objets géométries plus concrets.

Je lis ce lien http://www.math.jussieu.fr/~leila/grothendieckcircle/deligne.pdf

Si j'ai un truc expliquable, je le dirai.

[barbu23]

Ta question m'embêtes un peu.
.

Pourquoi, elle t'embete ? :happy3:
POurquoi, la deuxième flèche est surjective ? :happy3:

[Finrod]

Je suis resté sur la question de la droite affine...

J'étais resté page2, j'ai raté les 4 ou 5 derniers messages.

Donc comme le dit Doraki, en géométrie algérique, la droite affineest définie comme ça, mais il y a une raison à ce choix.

Et j'aimerai bien résussir à la retrouver.

[Finrod]

Bon, j'ai pas pour l'interprétaton géométrique.

Je suis trop algébriste, le point de vue géométrique, ça me parle pas trop.


Bon, par contre pour ton faisceaux, la définition est équivalent au fait de dire que F(U) est le noyau du morphisme



Donc la suite est exacte à gauche, au milieu (la composé des 2 morphismes est nulle) , mais pas à droite. Il a aucune raison d'être surjectif ce morphisme.

[barbu23]

Non, mais c'est par definiion d'une suite exacte courte non ? la dernière flèche à droite doit etre surjecti ve, la première à gauche doit etre injective et celle du milieu doit verifier l'egalité : , non ? :happy3:

[Finrod]

Oui en effet.

Mais dans ce cas, la suite exacte courte s'écrit

0 -> Truc -> Machin -> Bidule

Et on met pas de 0 à droite, parceque c'est pas exact.

Où as-tu lu que cette suite était exacte à droite ?

[barbu23]

D'accord ! j'ai mal recopié le paragraphe, c'est vrai, il n'y'a pas de zero à droite, donc, reste à montrer que ! :happy3:

[barbu23]

On montre que
Alors
soit
donc :
d'après, la condition de recollement donc , donc donc,
d'ou l'inclusion ! :happy3:

[barbu23]

Pour l'inclusion inverse : :happy3:
Soit , alors : , i.e : , d'après, la condition de recollments : : , donc
d'ou l'inclusion ! :happy3:

[barbu23]

J'ai une autre question à vous poser : :happy3:
Soit muni du faisceau : avec un ouvert de .
Soit :
Soit : avec : la relation d'equivalence definie par : :

POurquoi : est la limite inductive des ?
Merci d'avance ! :happy3:

[Finrod]

POurquoi : est la limite inductive des ?

?

Tout objet est limite inductive de lui même, au moins en un certain sens.

What is the question ?

[barbu23]

?

Tout objet est limite inductive de lui même, au moins en un certain sens.

What is the question ?

désolé, j'ai corrigé, voiçi la question :
POurquoi : est la limite inductive des ? avec les contient

[Finrod]

Il s'agit en fait de la "fibre", ou du "germe" du faisceaux au point p.

Sa définition se fait via cette colimite filtrante.

Et quasiment par construction, cela revient au quotient que tu as donné avant.

ça peut se montrer à la main.

[barbu23]

La definition du germe du faisceau en comme tu l'expliques Finrod :
:
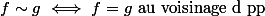
coincide avec la notion de limite inductive comme definie par exemple au milieu de la page suivante :
http://fr.wikipedia.org/wiki/Limite_inductive
Sauf que j'ai du mal à comprendre pourquoi il faut une union disjointe des elements du système inductif : :happy3:
Merci de votre aide ! :happy3:

[Finrod]

Parceque, avant de quotienter, on veut un objet libre de toutes contraintes.

Les contraintes, on veut les choisir via le quotient que l'on fait.

[barbu23]

c'est pas encore evident pour moi, sinon, quel lien a celà avec la fibré tangent qui est une union disjointe d'espace tangent au voisinage de ? :happy3: