Endomorphismes symétriques et orthogonaux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 24 Jan 2015, 18:57
par mamas67 » 24 Jan 2015, 18:57
Bonjour,
Alors voilà : j'ai f(x)= 2/*u -x, où u est un vecteur non nul d'un espace euclidien E muni du produit scalaire < , >, et x appartient à E
On me demande de montrer que f est un endomorphisme orthogonal et symétrique.
Le coté endomorphisme ( et linéaire ) de l'application me pose pas de soucis
Par contre pour montrer que f est orthogonal ( c'est à dire que < f(x),f(y) > = < x,y > )
et que f est symétrique ( c'est à dire que < f(x),y > = < x,f(y) > ) je bloque un peu :
J'ai retourné les expressions dans tous les sens, mais je m'emmêle les pinceaux avec tous les produits scalaires ..
Une petite aide ne serait pas de refus =]

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 24 Jan 2015, 19:18
par zygomatique » 24 Jan 2015, 19:18
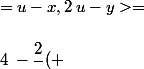 + =)
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Jan 2015, 11:25
par mamas67 » 25 Jan 2015, 11:25
Je comprends qu'à moitié ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
