Endomorphismes nilpotents

par **pouik** » 30 Sep 2007, 15:00

Bonjour,
J'ai quelques difficultés sur certains points de cet exercice, pourriez-vous m'aider à les surmonter ? Merci par avance.

Soit

un K-espace vectoriel de dimension

, soit

un endomorphisme nilpotent (il existe un entier natuel

tel que

).
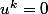
1. Soit

un vecteur de

. Soit

le plus petit entier naturel tel que

(justifier son existence). Montrer que la famille

est libre. En déduire que

.
2. On suppose de plus que

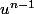
différent de

(justifier l'existence de tels endomorphismes). Montrer que l'endomorphisme

n'admet pas de racine carrée (c'est-à-dire qu'il n'existe pas d'endomorphisme

de

tel que

).

par **pouik** » 30 Sep 2007, 15:04

Pour l'existence de

est-ce que si je dis que :

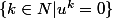
est un ensemble non vide et minorée par

donc il admet une borne inférieure qui est atteinte puisqu'on manipule des entiers donc il existe un plus petit entier

tel que

.

est-ce correct ??

par **Joker62** » 30 Sep 2007, 15:24

Pas besoin de minoration
On est dans N
Toute partie non vide possède un plus petit élément.

par **pouik** » 30 Sep 2007, 15:43

Ok.
Ensuite, supposons que :

en composant par

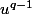
qui est différent de

car

est le plus petit entier tel que

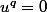
, donc a fortioiri on a bien

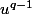
différent de

.

donc :

soit

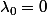
on compose par

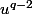
et on trouve que

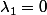
... donc la famille est libre.

Est-ce correct ??

Par contre je ne vois pas comment déduire de ceci que

:hum: :hum:

par **yos** » 30 Sep 2007, 15:52

C'est correct.
Après si

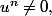
tu aurais q>n et donc un peu trop d'éléments ds une famille libre.

par **pouik** » 30 Sep 2007, 16:20

D'accord.
Pourriez-vous m'aider pour la 2. car je ne vois pas comment procéder.

par **yos** » 30 Sep 2007, 16:43

Par l'absurde : en appliquant le résultat de la 1 à f.

par **pouik** » 30 Sep 2007, 16:58

yos a écrit:Par l'absurde : en appliquant le résultat de la 1 à f.

désolé mais je ne comprends pas bien en quoi consiste ce que vous me proposez. :hum: :hum:

par **yos** » 30 Sep 2007, 17:16

On suppose que

.
On a donc

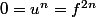
donc f est nilpotente, donc

, donc
- si n est pair,

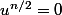
impossible.
- si n est impair,

impossible.

par **pouik** » 30 Sep 2007, 17:22

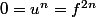
yos a écrit:On a donc donc f est nilpotente, donc ,

vraiment désolé mais je ne comprends pas en quoi le fait que

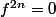
implique que

. :marteau: :marteau:

Sinon comment justifie t-on qu'il existe des endomorphismes tels que

différent de 0.

Merci d'avance pour votre aide.

par **yos** » 30 Sep 2007, 17:26

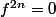
pouik a écrit:vraiment désolé mais je ne comprends pas en quoi le fait que implique que

Mais tu l'as prouvé dans la question précédente : dés qu'un endo u est nilpotent, on a

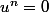
. Ici il s'appelle f. Ca gène pas.

pouik a écrit:Sinon comment justifie t-on qu'il existe des endomorphismes tels que différent de 0.

On en exhibe un sous forme matricielle : des 0 partout sauf sur la surdiagonale où on met des 1.

par **pouik** » 30 Sep 2007, 17:43

d'accord mais pour la matrice quelle taille a t elle ? et la surdiagonale, est-ce que ca signifie diagonale + triangle supérieur ?

par **yos** » 30 Sep 2007, 17:52

la surdiagonale a pour équation j=i+1.
La taille de la matrice est n bien sûr.

par **pouik** » 30 Sep 2007, 18:03

merci pour votre aide

Endomorphismes nilpotents

Endomorphismes nilpotents

Qui est en ligne