Endomorphismes nilpotents

[jose_latino]

Si alors

1. pas de problème.
2. alors

[jose_latino]

dans la premiére démo que j'ai essayé de faire je voulais montrer qu'on a une famlle libre de n+1...

L'idée de la prémière méthode est supposer que . (donc ). Alors il existe tel que , donc on va considérer l'ensemble . Soit le mineur tel que , alors et . Affirmation: est une base de .
Si . On applique est on obtient , ça veut dire que , après on continue avec etc, jusqu'à ... Comme est une base de , alors , donc est invertible. C'est une contradiction.

[Alpha]

Salut, apparemment othoo, tu n'as pas vu où je voulais en venir, je vais donc te donner ma solution complète (mais peut-être n'as-tu pas vu le polynôme minimal?) :

S'il existe k tel que f^k = 0, alors le polynôme minimal de f divise X^k, donc il est de la forme X^p avec p divisant k, mais le degré du polynôme minimal est de degré inférieur ou égal à n, donc ,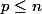
donc f^n = (f^p) o f^(n-p) = 0.

[jose_latino]

Désolé Alpha, mais à mon avis, utiliser la théorie du polynôme minimal pour ce problème est un peu excesif.

[othoo]

salut alpha dans ta démo utilisant la polynôme minimal je ne vois pas pourquoi p doit diviser k je crois que p<(ou égale)k suffit

[sandrine_guillerme]

Salut ..
Si Si .. p doit diviser k .. mais je commence à croire que je n'aurais pas du parler de polynome minimal..
Vous en avez parler du polynome minimale .. as tu deja travailler des exercice de ce type .. si ta vraiment du mal a comprendre skon dit ..
tien ce lien a été poster par un memebre de forum il contient d'exelent cours ..
http://www.sciences.ch/dwnldbl/mathematiques/telecharger.php3

regarde la dessus et quand t'aura pas compris .. là tu risque d'alez plus loin avec tes raisonnement .. Allez A+