Endomorphismes nilpotents

par **othoo** » 19 Sep 2006, 21:05

bonjour j'ai une question que je n'arrive pas à demontrer même si elle semble évidente:si E est un espace vectoriel d dimension finie n , et f un endomorphime de E .on suppose qu'il existe un entier k tel que f^k=0
montrer que f^n=0 merci

par **sandrine_guillerme** » 19 Sep 2006, 21:10

Bonjour,
Nous souhaitons que vous ayez d'abord une idée .. c'est tout simple ..
indice: pense aux familles .
Bon courage

par **jose_latino** » 19 Sep 2006, 21:12

Tu peux trouver une idée semblable ici . Suppose que

alors il existe

tel que

, suis l'idée du lien. :id:

par **sandrine_guillerme** » 19 Sep 2006, 21:15

jose_latino a écrit:Tu peux trouver une idée semblable ici . Suppose que alors il existe tel que , suivi l'idée du lien. :id:

Je ne suis pas tout à fais d'accord avec toi dans la mesure ou on multiplie par x .. je serais toi je suggérerais de supposer que la famille (T1....Tk) liée et on trouve l'indice de nilpotence en prouvant a un certain k elle serais libre .. on se ramenrais donc a calculer le polynome minimal koi.

par **jose_latino** » 19 Sep 2006, 21:18

À mon avis, c'est pas nécessaire utiliser une chose comme le polynôme minimal. As tu essaié la solution que je proposse?. C'est pas nécessaire de parler de l'indice de nilpotence pour cet exercice aussi.

par **sandrine_guillerme** » 19 Sep 2006, 21:21

jose_latino a écrit:À mon avis, c'est pas nécessaire utiliser une chose comme le polynôme minimal. As tu essaié la solution que je proposse?. C'est pas nécessaire de parler du indice de nilpotence pour cet exercice aussi.

Ah yes ! :id:
tu a raison .. je viens de voir ..
mais essais mon idée .. ça saute aux yeux .. on pourrais naïvement être conduit au calcul matriciel dans la pratique si tu vois bien ce que je veux dire

par **jose_latino** » 19 Sep 2006, 21:26

Je suis intéressé à ton idée, tu dis que

serait libre, où l'indice de nilpotence est

, je sais que le polynôme minimal de

est

, je ne comprends pas qu'est-ce que tu veux dire?. :briques:

par **sandrine_guillerme** » 19 Sep 2006, 21:36

c'est tout ! quitte à supposer une matrice appartenant a l'endomorphisme donc A^n verifiera la relation souhaité.. Oups on aura tout souflé au jeune homme.. à lui de jouer.. quoique je lui conseille de suivre ce que tu a proposer ..
:happy2:

par **Alpha** » 19 Sep 2006, 22:15

Eh bien oui si f^k = 0 le polynome minimal de f divise X^k, donc il est de la forme X^p avec p divisant k, mais le polynôme minimal est de degré inférieur ou égal à n... Je laisse la conclusion à celui qui a posé la question...

A+ :lol4:

par **othoo** » 20 Sep 2006, 15:18

bonjour, voici la méthode que j'ai essayé mais elle n'a rien donné
si n>k f^n=f^(n-k)of^k=0
si non suppose qu'il existe xappartenant à E tel que
(f^n)(x)est différent de 0 alors pour tout k entre 0 et n (f^k)(x) est différent de o
ce que je veux montrer c'et que la famille x,f(x),....,f^(x) est libre dans un
espace vectoriel de dimension n ce qui est absurde
soit a(0),......a(n) des réels tels que
a(0)x+.......a(n)(f^n)(x)=0
par l'absurde je suppose que les coeficients sont non tous nuls
alors I=l'ensemble des entiers K entre 0 et n tels que a(k) est different de0
est non vide donc admet un petit élement p
donc a(p)(f^p)(x)+...........a(n)(f^n)(x)=0
je veux monter que a(p)=0 mais j'arrive pas merci

par **sandrine_guillerme** » 20 Sep 2006, 16:15

sandrine_guillerme a écrit:c'est tout ! quitte à supposer une matrice appartenant a l'endomorphisme donc A^n verifiera la relation souhaité.. Oups on aura tout souflé au jeune homme.. à lui de jouer.. quoique je lui conseille de suivre ce que tu a proposer ..
:happy2:

Alpha a écrit:Eh bien oui si f^k = 0 le polynome minimal de f divise X^k, donc il est de la forme X^p avec p divisant k, mais le polynôme minimal est de degré inférieur ou égal à n... Je laisse la conclusion à celui qui a posé la question...

A+ :lol4:

suis ce chemin à toi de conclure!
A+

par **jose_latino** » 20 Sep 2006, 16:19

othoo a écrit:bonjour, voici la méthode que j'ai essayé mais elle n'a rien donné
si n>k f^n=f^(n-k)of^k=0
si n<k par l'absurde
on suppose qu'il existe xappartenant à E tel que
(f^n)(x)est différent de 0 alors pour tout k entre 0 et n (f^k)(x) est différent de o
ce que je veux montrer c'et que la famille x,f(x),....,f^(x) est libre dans un
espace vectoriel de dimension n ce qui est absurde
soit a(0),......a(n) des réels tels que
a(0)x+.......a(n)(f^n)(x)=0
par l'absurde je suppose que les coeficients sont non tous nuls
alors I=l'ensemble des entiers K entre 0 et n tels que a(k) est different de0
est non vide donc admet un petit élement p
donc a(p)(f^p)(x)+...........a(n)(f^n)(x)=0
je veux monter que a(p)=0 mais j'arrive pas merci

L'ensemble est

(sinon cet ensemble aurait n+1 éléments).
Utilise une autre lettre différente de k. On a qu'il existe

tel que

. On suppose que

. La petite astuce est considérer le mineur

tel que

, naturellement

. Cette condition entraîne que

. Alors si tu as:

. Qu'est-ce qui se passera si tu appliques

à cette équation?. Je crois que tu arriveras. Bon courage!

par **jose_latino** » 20 Sep 2006, 16:27

Une autre méthode: Si tu as qu'il existe

tel que

alors, soit

le mineur nombre naturel tel que

. Alors tu as que

. Comme avant prends un élément

tel que

. C'est possible prouver que

est lineairement indépendant. Comme

, alors

. Donc tu as déjà la réponse.

Les deux méthodes sont semblables mais ils ne sont pas égaux. J'espère que tu aies compris sinon tu peux nous demander avec confiance. À plus! :zen:

par **othoo** » 20 Sep 2006, 19:18

bonsoir, j'ai une petite question un peu bête si on a f^(n)=0(avec f endomorphisme) est ce que cela veu dire que pour tout x de E a (f^n)(x)=0
ou bien il existe x tel que (f^n)(x)=0 merci

par **sandrine_guillerme** » 20 Sep 2006, 19:22

Pour tout x de E

par **othoo** » 20 Sep 2006, 19:43

est ce que le raisonement que j'ai fait est faux, vraiment j'ai pas compri la démonstration qui consiste à considérer un mineur....

par **jose_latino** » 20 Sep 2006, 20:02

je parlerai de façon plus détaillé, (la deuxième méthode)
Par hypothèse, tu as qu'il existe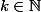

tell que

(c'est une équations entre fonctions, ça veut dire:

pour tout

).
Voici le raisonement détaillé: Considère le sous-ensemble

de

.

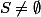parce que quand même

. Tout sous-ensemble non vide de

posède un élément minimum (principle du bon ordre). Qu'est-ce que cela signifique?, ça signifique qu'il existe

tel que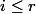

pour tout

. Tu prouver comme exercice le suivant:

Soit

.

est l'élément minimun de

entraîne que:

ou

j'ai utilisé ce résultat sans le dire. Mais à mon avis c'est un peu plus facil du croire intuitivement.

Alors, on a pris

comme le minimum de

. Justement, j'ai utilisé le résultat de l'exercice:

ou

ça veut dire que

et

, après tu peux continuer la preuve. Contacte-moi s'il y a un autre doute. Bonne chance! :happy2:

par **othoo** » 20 Sep 2006, 20:49

j'ai pas compri pourquoi i-1<(ou égale)n implique f^n=0 j'ai du mal vraiment j'ai pas l'habitude d'utiliser des raisonnements pareil

par **jose_latino** » 20 Sep 2006, 20:57

Je suis désolé, correction, il faut analyser

(pour cette deuxième méthode). J'ai fait la correction, relis s'il te plaît. :marteau:

par **othoo** » 20 Sep 2006, 21:12

dans la premiére démo que j'ai essayé de faire je voulais montrer qu'on a une famlle libre de n+1 élements dans un espace vectoriel de dimension n ce qui est absurde ...dans votre démonstration vous avez fait une raisonnement directe mais je ne vos pas pourquoi i<(ou égale à n) implique f^n=0

Endomorphismes nilpotents

endomorphismes nilpotents

Qui est en ligne