Endomorphisme ..

[sandrine_guillerme]

tout à fait! bien vu Joker !!!

à part la nilpotence on ne peut rien dire?

[serge75]

Je ne m'y serais pas pris comme ça, j'avais une autre idée. Je vous la poste ce soir si j'y pense, mais là je suis à la bourre.
Serge

[Joker62]

Donc mise à part la nilpotence.

On voit que 0 est valeur propre double.
Donc u n'est pas injective.

[sandrine_guillerme]

Je ne m'y serais pas pris comme ça, j'avais une autre idée. Je vous la poste ce soir si j'y pense, mais là je suis à la bourre.
Serge

oki serge,
on t'attends ce soir lol ..

[sandrine_guillerme]

Donc mise à part la nilpotence.

On voit que 0 est valeur propre double.
Donc u n'est pas injective.

pas la peine d'aller jusque là au fait , le fait que le det est nul montre directement qu'elle est pas bijective donc pas injectif

[Joker62]

En plus lol :)
Mais non bijectif n'entraîne pas non injectif.

Plutot non injectif OU non surjectif mais bon je chipotte je sais lol :D

[sandrine_guillerme]

Voyons joker on a le même espace là, d'arrivée et de départ
l'une est equivalente à l'autre !

[Joker62]

Mon dieu ! :)
Je vais me laver lol :D

[sandrine_guillerme]

allez un autre exo (en attendant que serge arrive )bien plus sympa aussi sans aucune difficulté particulière mais qui fais réfléchir

enconcé:
M la matrice suivante
(0 0 0)
(0 0 1)
(0 0 0)
1/ on suppose que v d'ordre 2 et la dim du noya est 2. supposons a n'est pas élèment du noyau de v. construire à partir de a et v(a) une base dans la quelle la matrice de v est M.

2/ supposons v nilpotent d'ordre 2 et dim du noyau de v est 1
on considère la base telle que élement du noyau de v
a/ Montrer qu'il existe 2 réelles lambda et mu tel que et .

b/Montrer que si est non nul alors élement de ker(v).
c/en déduire que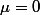 . que peut on conclure .


bonne gymnastic .

[serge75]

Bon la voilà mon autre méthode :
determinant et traces nulles équivalent pour un endo de R3 équivaut à dire que son polynôme caractéristique est du type X^3+aX.
Si a=0, ça ne nous fait pas un contre exemple d'après les sieurs Cayley et Hamilton.
Donc je vais construire mon endo à l'envers en coisissant d'abord son polynôme caractéristique ; je décide par exemple que je veux X^3-X=X(X²-1).
Il suffit pour cela de prendre la matrice diagonale diag(0,1,-1) et c'est plié !
(avec un minimum d'intuition on pouvait directement exhiber une telle matrice sans passer par ma théorie. Si on veut frimer, on la tord par une matrice P^(-1) à gauche et une matrice P à droite pour en sortir une bien compliquée).
Serge.

PS : j'avais proposé une extension de l'exo de Sandrine, mais qui ne semble pas avoir eu de succès... lol

[sandrine_guillerme]

Très bien Serge, nous voilà avec une nouvelle méthode !
mais rassures toi il aurra un succès ton extention de l'exo là ..

voici l'exo

je l'ai pas trouvé mais voici un biensympa aussi ..
SOit E =R^3. soit u un endomorphisme annulé par P(X) =X^3+X
posons v= (X^2+1)(u)

1/Exprimer v(x) en fonction de u(x) et x.montrer que uov=0
2/ Soit x un vecteur de E. On pose y= -u^2(x) et z = x-y. montrer que y élement de ker (v) et z élèment de ker (u) . et en déduire que E=ker (u) + ker(v).
3/ Montrer que la somme E = Ker(u)+ker (v) est directe .

jusque là c'est bon ..

voici ou on en est

Si on suppose de plus que u et u²+1 ne sont pas inversibles, montrer qu'il existe une base dans laquelle la matrice de u est
0 0 0
0 0 1
0 -1 0
Donner un contre exemple si K=C.

sans oublier le " hihihihih"

[Joker62]

J'avoue la suite de l'exo m'inspire pas :^)

[sandrine_guillerme]

allez je prends le relais
Serge il faut montrer l'existence sans l'expliciter ?

[serge75]

L'énoncé ne demande pas d'expliciter... Ceci dit l'idée de résolution que j'en ai est pas mal explicite.

[sandrine_guillerme]

alors déjà une chose pas mal, on a bien un contre exemple (un bon) de ce qui a été déjà dis .. en premier exercice.. trace nulle et dét nul et pourtant l'endorphisme n'est pas nilpentent certes, mais il est injectif, donc à mon avis on cherche une base de l'image ?

suis je sur la bonne voie?

[serge75]

euh, sandrine, là je suis plus du tout...
De quel endomorphisme parles-tu ?

[sandrine_guillerme]

je ne me suis pas bien exprimée ...
récapitulons,
l'exercice que j'avais proposais au début (un endomrphisme de déterminant et de trace nulle dans R^2 on a dis que la matrice associé serait nilpotente ..

pour R^3 tu nous avais demandais un contre exmple joker t'en avais donné un. et moi j'ai dis voici un contre exemple d'une matrice qui a une trace nulle, et un déterminant nul et qui n'est pas nilpotente ..

tu me suis?

[serge75]

La matrice
0 0 0
0 0 1
0 -1 0
de déterminant nul ????

[sandrine_guillerme]

pas du tout ,j'ai raconté une très belle connerie !



désolée !

[serge75]

C'est bien ce qu'il m'avait semblé :we:
Tu me copieras dix fois : une matrice dont une ligne ou une colonne est nulle a son déterminant nul (et pas de copié collé, hein) :briques:
hihihihihihihi