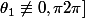Endomorphisme normal

[girdav]

Bonjour.
Je recherche une démonstration du théorème suivant :

Soit un endomorphisme nomal de . Alors il existe
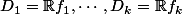
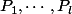
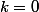
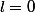
, des plans (avec éventuellement ou tel que :
1 )

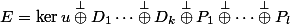
2)

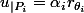
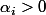
3) avec et

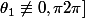
Mon prof a fait une récurrence sur la dimension de .
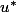
Mais le passage sur la démonstration de l'existence d'un plan stable par et est assez flou.
C'est pourquoi je fais appel à vous, au cas où vous connaîtriez une référence qui traite le sujet.
Merci d'avance!

[Nightmare]

Salut !

Ca ne me semble pas vrai si u admet une valeur propre ! Par contre on peut dire qu'il existe un plan ou une droite stable par u et son adjoint.

Déjà, l'existence d'un plan ou d'une droite de u est "claire". Si u admet une valeur propre on prend la droite engendrée par un vecteur propre. Sinon, utliser Cayley-Hamilton pour montrer l'existence d'un plan stable par u.

Ensuite il suffit de montrer que tout espace stable pour u l'est aussi pour son adjoint, pour cela, regarder les matrices de u et u* dans une base formée d'une base d'un espace stable puis de son complémentaire.

[girdav]

En fait on peut aussi le démontrer en utilisant la complexification: l'extension sera normale, donc diagonalisable dans . On pourra se débrouiller à partir de ça.