Endomorphisme et inversibilité

[jonses]

bonjour ou bonsoir,

J'essaye de faire un exercice, mais j'ai passé un bon moment sans aboutir à quoi que ce soit.


---

Soit un C-ev de dimension finie
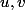
Soient deux endomorphismes de E

On suppose que et commutent et que

Je dois montrer qu'il existe tel que est inversible


---

J'ai essayé entre autres par l'absurde, mais je n'arrive pas à aboutir à une contradiction. J'ai essayé de passer par les déterminants, mais j'aboutis pas. Sinon j'ai essayé de chercher "à la main" à l'aide des hypothèse, de la formule du rang, de la finitude de la dimension de E, etc... mais c'est très dispersé et la plupart du temps je m'éloigne vite de ce qui est demandé.


Si quelqu'un peut me donner une petite indication svp.
Je vous remercie d'avance pour vos réponses

[Joker62]

Hello,

On est dans C, les endomorphismes u et v commutent donc ils sont co-trigonalisables.

ça veut dire qu'ils existent une même base de vecteurs propres qui trigonalise u et v.

Tu peux alors calculer le déterminant de u+tv plus facilement.

[jonses]

Merci !

C'est en effet assez simple de calculer le déterminant de u+tv, mais je reste encore bloqué en fait.
J'ai du mal à utiliser l'hypothèse

J'ai essayé de montrer que ce n'est pas possible d'avoir : det(u+tv)=0
car sinon on aurait (grâce au calcul "plus simple" du det(u+tv)) det(u)=det(v)=0
du coup u et v auraient un vecteur propre commun dans et un autre en commun dans , mais je n'arrive pas à montrer que dans ce cas est non réduit au singleton 0, ce qui permettrait de mettre en avant une contradiction et donc de conclure

[Joker62]

En fait on a :

det avec valeur propre de u et valeur propre de v.

Ce déterminant est un polynôme en t. S'il est nul, c'est qu'il y a forcément un facteur nul.
C'est à dire sans perdre de généralité que

Il reste à trouver une contradiction avec

[jonses]

En fait on a :

det avec valeur propre de u et valeur propre de v.

Ce déterminant est un polynôme en t. S'il est nul, c'est qu'il y a forcément un facteur nul.
C'est à dire sans perdre de généralité que

En fait, c'est ce que je voulais exprimer, mais comme je n'avais pas le temps ce matin pour l' écrire en LaTex (j'écris lentement en LaTex), j'ai essayé de l'expliquer à l'aide d'un pâté de mots, mais finalement ce n'était pas clair.

Il reste à trouver une contradiction avec

C'est bien ce que j'essaye de faire, mais je n'ai pas réussi à l'aide des valeurs propres (ça fait depuis un bon moment que je n'avance pas)

[Joker62]

Bé le problème c'est qu'ils ont forcément un vecteur propre associé à 0 en commun sinon on ne pourrait pas les trigonaliser simultanément...

[jonses]

Bé le problème c'est qu'ils ont forcément un vecteur propre associé à 0 en commun sinon on ne pourrait pas les trigonaliser simultanément...

Désolé, mais ça, ça m'échappe un peu. J'ai vraiment du mal à voir pourquoi on a forcément un vecteur propre commun associé à 0 ?
Tout ce que j'ai vu pour la co-trigonabilité, c'est qu'il existe une base B telle que u ait pour matrice dans B une matrice triangulaire supérieur, et de même pur v