Encore du polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
par fenecman » 02 Jan 2008, 15:37
bonjour!
Bon voilà cet exercice j'ai compris le mécanisme, je vois le truk mais j'arrive pas le formaliser (je sens venir des permutations alors j'arrete !!):
soit P un polynome de C[X], de degré n superieur ou égal à 2, ayant n racines distinctes x1, x2 ,... , xn
il faut montrer que
}=0)
Merci
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 02 Jan 2008, 17:35
Joli !
Une solution (très très très) indirecte (mais qui marche quand même donc en attendant mieux ...) :
Il est facile de montrer que :
} \frac {1}{X-x_i})
d'où
} \frac {X}{X-x_i})
On considère ça comme une fonction définie sur
et on fait
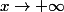
On obtient bien
})
par busard_des_roseaux » 02 Jan 2008, 17:59
ThSQ a écrit:On considère ça comme une fonction définie sur
et on fait
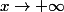
On obtient bien
Pas de souçi,
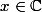
et
-
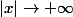
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
par fenecman » 02 Jan 2008, 18:16
ThSQ a écrit:Joli !
Une solution (très très très) indirecte (mais qui marche quand même donc en attendant mieux ...) :
Il est facile de montrer que :
d'où
On considère ça comme une fonction définie sur
et on fait
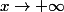
On obtient bien
Rapide la méthode !!! Comme quoi pas la peine de se fatiguer sur des solutions trop laborieuses !!!
Juste quand tu dit qu'il est facile de montrer etc... , tu decomposes en élément simple la fraction rationelle 1/P c'est ça?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 02 Jan 2008, 18:19
fenecman a écrit:tu decomposes en élément simple la fraction rationelle 1/P c'est ça?
'xactement.
Merci busard_des_roseaux, j'avais eu un gros doute d'un coup sur la légalité de la limite sur
par busard_des_roseaux » 02 Jan 2008, 20:04
ThSQ a écrit:'xactement.
Merci busard_des_roseaux, j'avais eu un gros doute d'un coup sur la légalité de la limite sur
de rien,
est normé,complet,localement compact.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 03 Jan 2008, 00:11
Variante :
=(X-x_n)Q(X))
,
=Q(X)+(X-x_n)Q'(X))
donc
}=\sum_{k=1}^{n-1}\frac{1}{(x_k-x_n)Q'(x_k)}+\frac{1}{Q(x_n)})
et on conclut avec la décomposition en éléments simples de 1/Q.
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
par fenecman » 03 Jan 2008, 10:50
Il fallait y penser quand meme à cette décomposition en élément simple !!!
La seule relation que j'avais entre P et P' c'était
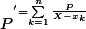
, j'avais jamais vu l'autre. Tant mieux !
Si je suis en train de passer à côté d'autre relations " a connaître" dites moi !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 03 Jan 2008, 11:12
Peut-on généraliser ??
Que vaut
})
pour N < d°P
Réponse :
oui on peut 
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
par fenecman » 03 Jan 2008, 12:14
Dans la somme c'est
)
ou
)^N)
?
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 03 Jan 2008, 14:42
fenecman a écrit:Dans la somme c'est
ou
?
.
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 03 Jan 2008, 15:23
ThSQ a écrit:Joli !
Une solution (très très très) indirecte (mais qui marche quand même donc en attendant mieux ...) :
Il est facile de montrer que :
d'où
On considère ça comme une fonction définie sur
et on fait
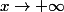
On obtient bien
busard_des_roseaux a écrit:de rien,
est normé,complet,localement compact.
Arf, ça me choque toujours quand un argument (tout à fait correct, certes) d'analyse ou topologique sert à prouver quelque chose sur C, alors que le résultat (100% algébrique) est valide sur tout corps... avec le même raisonnement ! (sauf à la fin bien sûr.) Il y a d'autres exemples du même genre dans l'enseignement, où on utilise la densité, etc. Arf, ça me choque... :ptdr:
Ok revenons à l'exo, après l'
existence de la décomposition en éléments simples de
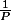
on arrive à
on écrit
} \frac {X-x_i+x_i}{X-x_i} = \sum \frac {1}{P'(x_i)} + \sum \frac {1}{P'(x_i)} \frac {x_i}{X-x_i})
et on conclut avec
l'unicité de la décomposition en éléments simples
de
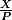
(sans terme constant puisque P est de degré >1).
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
par fenecman » 03 Jan 2008, 20:06
ThSQ a écrit: .
J'aurais pensé à du
^N})
mais ça colle pas, mais j'ai pas envie de me rendre tout de suite!! :hum:
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 03 Jan 2008, 21:07
ThSQ a écrit:Peut-on généraliser ??
Que vaut
pour N < d°P
En voulant généraliser
})
, on arrive directement (avec la même preuve un poil modifiée) à
}{P'(x_i)})
pour tout polynôme Q avec
 < deg(P))
.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 03 Jan 2008, 21:33
leon1789 a écrit:En voulant généraliser
, on arrive directement (avec la même preuve un poil modifiée) à
pour tout polynôme Q avec
.
Pas tout à fait !
Je t'invite à regarder attentivement le cas d°Q = d°P - 1
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 03 Jan 2008, 22:59
Oui c'est vrai, j'ai commis une "petite étourderie". Mais je vais me corriger.
Après l'existence de la décomposition en éléments simples de
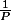
on arrive à
}{P(X)} = \sum \frac {1}{P'(x_i)} \frac {Q(X)}{X-x_i})
On écrit
}{P(X)} = \sum \frac {1}{P'(x_i)} \frac {Q(X)-Q(x_i)+Q(x_i)}{X-x_i} = \sum \frac {1}{P'(x_i)} \frac {Q(X)-Q(x_i)}{X-x_i} + \sum \frac {1}{P'(x_i)} \frac {Q(x_i)}{X-x_i})
Par ailleurs,
-Q(x_i)}{X-x_i})
est un polynôme (division exacte), notons le
)
:
}{P(X)} = \sum \frac {1}{P'(x_i)} T_i(X) + \sum \frac {1}{P'(x_i)} \frac {Q(x_i)}{X-x_i})
On utilise alors l'unicité de la décomposition en éléments simples de
}{P(X)})
, de partie polynomiale nulle lorsque
 [TEX]0 = \sum \frac {1}{P'(x_i)}\frac {Q(x_i)-Q(0)}{x_i})
lorsque
.
En particulier, on a
})
pour
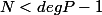
Pour
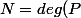 -1)
, on obtient non pas 0, mais le rapport des coefficients dominants de P et Q.
C'est ok, cette fois ? :we:
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
par fenecman » 04 Jan 2008, 10:55
Elle est jolie cette formule !!
Au moins j'aurais révisé les fractions rationnelles ( l'unicité de la decomposition en éléments simples j'avais oublié :ptdr: )
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 04 Jan 2008, 11:08
leon1789 a écrit:Oui c'est vrai, j'ai commis une "petite étourderie". Mais je vais me corriger.
Mais non, c'est pour voir si on suivait !
C'est bon maintenant :++:
Belle rédaction sinon , j'en prends de la graine.
par busard_des_roseaux » 04 Jan 2008, 16:53
Cher Léon1789,
est-ce que tu connais une démo du thm de D'alembert-Gauss (C algébriquemt clos) purement algébrique ? sauf erreur, il n'y en a pas. Les démonstrations
comportent toutes de l'analyse.
-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
par leon1789 » 04 Jan 2008, 17:35
busard_des_roseaux a écrit:Cher Léon1789,
est-ce que tu connais une démo du thm de D'alembert-Gauss (C algébriquement clos) purement algébrique ? sauf erreur, il n'y en a pas. Les démonstrations
comportent toutes de l'analyse.
Je m'y attendais... :we: Oui, c'est vrai.
Cela dit, ça me choque un peu quand même. :happy2: Et la preuve "absolue" que c'est choquant, c'est qu'on a essayé de faire une preuve sans analyse ! Si ce n'était pas choquant, on n'y aurait pas fait attention, si ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
