Encore un polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
eTom_06
- Messages: 2
- Enregistré le: 31 Aoû 2007, 14:57
-
 par eTom_06 » 03 Sep 2007, 10:20
par eTom_06 » 03 Sep 2007, 10:20
Bonjour,
Je dispose de la fonction qui exprime y en fonction de x, soit

.
Je souhaite exprimer x en fonction de y, ce qui reviens à trouver la (les) racine(s) -dont j'impose le caractère réel- du polynome :
=-2x^3+3x^2-y)
(y est donc ici un paramètre.)
J'ai testé la méthode Cardan mais je ne trouve pas de solutions réalistes ! :triste: Merci si vous avez des idées, pistes ou même résolution !
J'ajoute que x et y sont compris entre 0 et 1 (ce qui aide à la détermination de déterminant).
Merci beaucoup de votre aide !
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 03 Sep 2007, 12:57
par Flodelarab » 03 Sep 2007, 12:57
Ce que tu fais, pour moi, n'a pas de sens.
Sais tu ce qu'est une fonction ?
Tu ne peux pas retourner plusieurs valeurs
ex: si y = 0 alors x=0 OU x= 3/2
Tu ne peux pas exprimer x en fonction de y
Quelle est la véritable question ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 03 Sep 2007, 13:04
par alben » 03 Sep 2007, 13:04
Bonjour,
Je pense que tu as pu vérifier par la méthode de Cardan que ton équation avait trois solutions réelles si y est dans [0,1].
Le plus simple est d'utiliser alors le passage par les fonctions trigo (méthode de Viete).
En posant a=arccos(1-2y), on arrive à quelque chose d'assez simple
x=0,5+cos[(a-2pi)/3]
la difficulté est de montrer quelle racine choisir...
PS Il n'y a pas de problème, Flodelarab, le domaine de définition de x et y ne permet qu'une seule racine. Autrement dit de [0,1]dans [0,1] la fonction est bijective
-
eTom_06
- Messages: 2
- Enregistré le: 31 Aoû 2007, 14:57
-
 par eTom_06 » 04 Sep 2007, 14:04
par eTom_06 » 04 Sep 2007, 14:04
Effectivement le tracé de
)
illustre bien la bijectivité de la fonction dans l'intervalle [0;1]. c'est ce qui me fait dire que je peux trouver la fonction "transposée" (je ne sais pas si ce terme est rigoureux, je ne pratique pas les maths tous les jours :soupir2:). Je peux ainsi vérifier graphiquement la solution que je trouve, puisqu'elle peut se tracer manuellement à partir de la première.
Avec la formule de Cardan + Viete j'ai effectivement 3 solutions réeelles sur ]0;1[ :
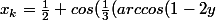+2k\pi))
avec

(elle sont supperposées)
Malheureusement le tracé graphique de cette fonction ne correspond pas du tout à ce à quoi on s'attend à partir de

.
Pour 0 et 1 j'ai un déterminant négatif, ce qui me permet de trouver des valeurs cohérentes (1;1), (0;0).
Suis-je dans les choux avec cette histoire de graphes ? :technicol
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Sep 2007, 14:24
par alben » 04 Sep 2007, 14:24
Bonjour,
Au lieu de transposée, utilise fonction inverse ou réciproque.
En ce qui concerne tes solutions, il n'est pas très difficile de montrer que pour k=1 ou 3, les solutions sont en dehors de [0,1].
La fonction arccos donne des valeurs dans [0,pi]
Par exemple avec k=1
+2\pi}{3}<\pi)
et
+2\pi }{3}) < -0,5)
et finalement -0,5<x<0 qui est hors du domaine accepté
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
