Encore des suites :p

par **nanou213** » 18 Sep 2006, 18:59

comment trouver une suite arithmétique vérifiant :
pour tout entier naturel
Un+1 +Un=n?

par **anima** » 18 Sep 2006, 19:07

nanou213 a écrit:comment trouver une suite arithmétique vérifiant :
pour tout entier naturel
Un+1 +Un=n?

Si il n'y avait pas ce n, je dirai raisonnement en cascade. Essaye quand même, qui sait

par **abcd22** » 18 Sep 2006, 19:11

Bonsoir !
Une suite arithmétique s'écrit

, essaie de déterminer a et r en utilisant l'hypothèse.

par **Quidam** » 18 Sep 2006, 19:15

nanou213 a écrit:comment trouver une suite arithmétique vérifiant :
pour tout entier naturel
Un+1 +Un=n?

Soit

une suite arithmétique de raison r :

Alors

et

La condition que doit réaliser ta suite se traduit alors par :

ou encore :

Donc...

par **oss007** » 20 Sep 2006, 09:11

bonjour,

On continue avec cet exercice: trouver toutes les suites vérifiant la relation de nanou213.
La moitié du chemin est déjà parcourue.
il s'agit d'un exercice d'Olympiades: je n'ai pas les références (année,pays) mais connais la solution.

bonne journée

par **xon** » 20 Sep 2006, 09:42

Salut,

que penses tu de ce raisonnement?

peut se réecrire

donc en posant

, on a que

est une suite arithmétique de raison -1/2 et donc on obtient

en rajoutant n/2 à

par **Quidam** » 20 Sep 2006, 11:08

xon a écrit:Salut,

que penses tu de ce raisonnement?

peut se réecrire donc en posant , on a que est une suite arithmétique de raison -1/2 et donc on obtient en rajoutant n/2 à

Pourquoi pas ? Mais ça paraît un peu parachuté par miracle ! Je ne suis pas certain que nanou213 appréciera ...

Je suis d'ailleurs étonné qu'il s'agisse d'un exercice d'Olympiades ! Je n'y connais pas grand chose, mais il me semblait que les exercices d'Olympiades étaient difficiles. Or celui-ci est vraiment facile...

par **xon** » 20 Sep 2006, 11:13

Désolé d'avoir posté la réponse directement.

L'idée c'est en fait de se dire qu'on peut découper le n qui est à droite en un terme en n+1 et un terme en n histoire de pouvoir poser facilement une nouvelle suite qui va etre plus simple (ici arithmétique), et donc c'est "naturel" d'écrire n=(n+1)/2 + n/2 -1/2 et de passer les termes en n à gauche.

J'espere avoir eclairée un peu ma démarche

par **oss007** » 20 Sep 2006, 12:59

bonjour xon,
ton résultat est donc : u_n = f(n), mais
peux-tu exprimer clairement ton f ?

Quidam : il y a une deuxième question à cet exercice.

par **xon** » 20 Sep 2006, 13:13

Désolé, j'ai pas fait les calculs jusqu'au bout.

Donc je disais que

vérifie

donc

, si je me souviens bien de l'expression d'une suite arithmético-géometrique

et donc

est ce que c'est çà?

par **Quidam** » 20 Sep 2006, 13:18

xon a écrit:Désolé d'avoir posté la réponse directement.

L'idée c'est en fait de se dire qu'on peut découper le n qui est à droite en un terme en n+1 et un terme en n histoire de pouvoir poser facilement une nouvelle suite qui va etre plus simple (ici arithmétique), et donc c'est "naturel" d'écrire n=(n+1)/2 + n/2 -1/2 et de passer les termes en n à gauche.

J'espere avoir eclairée un peu ma démarche

J'avais compris ! Simplement ta méthode, subtile et élégante, est un peu parachutée par l'esprit supérieur qui est le tien. Il n'est pas nécessaire d'utiliser une méthode aussi brillante pour résoudre un problème somme toute très élémentaire. Cela rejoint d'ailleurs ma remarque selon laquelle cet exercice ne mérite pas à mon sens de figurer parmi les exercices d'Olympiades, car ces derniers (on en a vus quelques exemples dans ce forum) sont le plus souvent redoutables !
En outre, vu le côté pédagogique de ce forum, je pense que nanou213 attendait une réponse la plus facile possible.

Mais j'admets que c'est très joli !

par **xon** » 20 Sep 2006, 13:20

on peut ecrire les choses de manière plus synthétique en donnant un nom à

on a donc

par **Quidam** » 20 Sep 2006, 13:20

oss007 a écrit:bonjour xon,
ton résultat est donc : u_n = f(n), mais
peux-tu exprimer clairement ton f ?

Quidam : il y a une deuxième question à cet exercice.

Où ça ?

Ca y est j'y suis, tu veux dire que c'est la suite de l'exercice qui le rend Olympiadisable ? Alors, donne nous la suite...

par **xon** » 20 Sep 2006, 13:23

Tu as raison Quidam ma méthode n'est pas très pédagogique, mais c'est que je répondait plutôt à la nouvelle question posée qui était trouver toutes les suites vérifiant cette relation

par **oss007** » 20 Sep 2006, 14:43

oui xon et merci pour ta méthode.

autre solution utilisant la question initiale de nanou213, ce qui avait d'ailleurs motivé ma question.
on a obtenu que les suites arithmétiques vérifiant la relation initiale sont les (U_n) tel que :
Un= n/2 - 1/4.

Soient une suite quelconque Vn vérifiant la relation initiale, et notre suite Un;
pour tout n, U_(n+1) + U_n = n et V_(n+1) + V_n = n
on soustrait ===> V_(n+1) - U_(n+1) = - (V_n - U_n).

puis , on pose suite (Tn) tel que : T_n = V_n - U_n ; par récurrence :
Tn = (-1)^n ( V_0 - U_0) avec U_0 = -1/4 ;finalement:
Vn= n/2 - 1/4 + (-1)^n .(V_0 - 1/4)

et ton écriture synthétique.

La deuxième question est:
Trouver alors un équivalent de x_n vérifiant pour tout n de lN : x_(n+1) =l x_n - nl ; ( lire valeur absolue )

question : pour écrire en latex, le $ ne marche pas ici ?

par **xon** » 20 Sep 2006, 16:15

Je donne juste une idée pour voir si vous êtes d'accord.

On va distinguer 2 cas pour simplifier

1) si

alors

et
2) si

alors

ce qui se passe c'est qu'on peut pas rester infiniment dans le cas 1) car aussi grand que soit

, dans le cas 1) on lui enlève n à chaque fois donc la suite va décroitre jusqu'à vérifier

et on passe ensuite dans le cas 2). (Il faudrait rédiger ceci plus proprement)

Il faut maintenant voir qu'une fois dans le cas 2) on y reste. En effet si

alors

donc par recurrence on reste dans le cas 2).

Ensuite on remarque que le cas 2) revient à

et que c'est justement la question traitée precedemment d'ou on déduit l'équivalent demandé qui est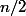

.

Voilà, qu'en pensez vous?

Ps: pour utiliser Latex utilise les bornes [TEX] à la place de $

par **oss007** » 20 Sep 2006, 17:04

rebonjour xon

c'est exact .

pour la première question , une autre réponse est :
[Tex] u_n=E[n/2] + (-1)^n.u_0[Tex]

Ref : "Des Olympiades à l'Agrégation" de M.Protat _ Ellipses, exo 73

C'est l'exo initial qui m'a fait penser à cette extension .

Si tu souhaites, j'en propose un autre sur les suites dans "Olympiades", mais cette fois , je ne connais pas la solution.

par **sandrine_guillerme** » 20 Sep 2006, 17:15

Bonsoir à tous!
pour méditer je travaille ces jours sur des exo d'olympiade .. J'ai les réponse .. alors si vous en avez envie de partager la joie de se casser la tete dites le moi et dites moi le domaine que vous souhaitez et on réfléchis ensemble !
Merci .

par **xon** » 20 Sep 2006, 17:58

Chouette exo en tous cas :we:

Pour les balises TEX tu as une icone juste au dessus du texte que tu tapes.

par **sandrine_guillerme** » 20 Sep 2006, 18:12

xon a écrit:Chouette exo en tous cas :we:

Pour les balises TEX tu as une icone juste au dessus du texte que tu tapes.

euh..? j'ai pas trop compris

Encore des suites :p

Encore des suites :p

Qui est en ligne