Je suis navré, je ne suis pas la bonne personne qui peut te conseiller. Dans ce fil, tu insistes sur la notion de dimension ( vers la fin ), et au début, tu parles de dimension topologique, dimension de Hausdorff, de Besicovitch, moi, j'ai même vu des probabilistes qui ont montré que la dimension de Minkowski ( si je ne m'abuse ) de certains courbes engendré par un mouvement Brownien est
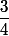
. Donc, pour étudier la dimension d'un objet, on a recours aux proba. , Ohh ! J'ai la tête qui tourne. :hum:
Bref, tu peux aborder tes constats de différents angles : proba. géométrie, topologie, algèbre ... etc. Bref, fonce, et essaye d'aller le plus loin possible, et trouver des connexions à plusieurs domaines à partir de ces constats. Plus, tu es confronté à plusieurs champs de travail, plus tu vois les choses de manière perçante, et pertinente. Reste à savoir, dans quel but tu comptes élargir ce travail que tu comptes mener. Est ce qu'il est en relation avec l'avancement de l'état actuel de la recherche en mathématiques, et ses objectifs majeurs. cela te permet d'être mieux encadré ,et tes recherches seront plus prises en compte, et mises en valeurs.
