Ellipses

[Pseuda]

Bonjour,

Le plan est muni d'un repère orthonormé. Soit les deux ellipses d'équations :

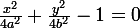
E1 : et E2 : .

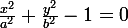
D'un point M de E1, on mène des tangentes à E2 qui rencontrent E1 aux points P et Q, distincts de M. Montrer que la droite (PQ) est tangente à l'ellipse E2.

Après quatre pages de calculs, j'arrive au résultat. Je ne vois pas comment on pourrait y arriver plus rapidement par des considérations géométriques ou autres. Merci d'avance.

[Manny06]

Peut-être en utilisant les cercles de centre 0 et rayon a et 2a,montrer la propriété pour les cercles et transformer ensuite la figure par une affinité orthogonale d'axe Ox et rapport b/a

[Ben314]

Salut,
Si tu considère l'application affine (x,y)->(ax,by) tes deux ellipses ont pour image deux cercles concentriques de rayon respectifs 2 et 1.
Evidement, les droites ont pour image des droites et l'application en question conserve la notion de "tangence" (il suffit de se dire par exemple qu'une droite et une ellipse sont tangente ssi elles ont un unique point commun)
Tu es donc ramené aux même problème avec deux cercles concentriques de rayon 2 et 1 et là, le résultat est trivial vu que, partant de M sur le grand cercle, les points P et Q que tu fabrique sont tels que le triangle (MPQ) est équilatéral (et les deux cercles sont respectivement le cercle inscrit et le cercle circonscrit du triangle équilatéral).

C'est un cas très particulier (avec une preuve extrêmement simple) de ce qu'on appelle le grand théorème de Poncelet (le cas général de deux conique quelconques est évidement bien plus difficile que le cas particulier de deux cercles concentriques)

[Pseuda]

Bonsoir,

Mais oui bien sûr, les cercles avec l'affinité orthogonale. Comment n'y ai-je pas pensé. Merci pour vos réponses.

Le triangle est équilatéral car il est isocèle (par symétrie), d'angle au sommet 60° (son sinus est de 1/2).

[Ben314]

Et si tu veut du "nettement plus difficile", tu part de deux cercles pas forcément concentriques :

Soit ABC un triangle quelconque, Ci son cercle inscrit et Cc son cercle circonscrit.

Partant d'un point M quelconque de Cc, on mène les deux tangentes à Ci passant par M et on note P et Q leurs deuxième points d'intersections respectif avec Cc (celui différent de M).
Montrer que la droite (PQ) est tangente à Ci.

[Pseuda]

Bonsoir,

Si on place M sur un des sommets du triangle, par exemple A, alors P et Q sont sur B et C, et (PQ) est tangente à Ci.

Si on déplace M sur le cercle, le cercle extérieur au triangle MPQ reste évidemment le même, mais pour le cercle intérieur, on peut seulement dire que le centre du cercle intérieur reste sur la bissectrice intérieure de l'angle PMQ.

Après, je ne saurais dire si le cercle intérieur reste le même, ou non.

[chan79]

Bonjour
Je reviens à l'énoncé initial. Pour ceux qui veulent chercher sans passer par les affinités:

I et J sont les points de contact des tangentes.
On peut montrer que comme la grande ellipse est l'image de la petite par une homothétie de rapport 2, I et J sont les milieux de [MP] et [MQ].
Or, on ne peut tracer qu'une seule ellipse connaissant son centre et deux tangentes avec les points de contact.
Dans le cas présent, c'est l'ellipse de Steiner du triangle MPQ et elle est tangente au troisième côté [PQ] en son milieu. Son centre est le centre de gravité de MPQ, c'est-à-dire l'origine du repère..

[Pseuda]

Bonsoir,

Je serais curieuse de savoir comment tu démontres :

On peut montrer que comme la grande ellipse est l'image de la petite par une homothétie de rapport 2, I et J sont les milieux de [MP] et [MQ].

Merci !

[chan79]

salut
tu devrais t'y retrouver avec cette propriété:
Si on trace des cordes parallèles à une tangente, leurs milieux sont alignés.


C'est sûr que c'est plus trop à la mode.

[Pseuda]

D'accord, mais je ne vois pas le rapport avec la démonstration de I milieu de [MP], ni d'ailleurs avec l'homothétie de rapport 2.

C'est une propriété qui n'est en effet plus trop à la mode, étant donné que les coniques ne sont plus au programme de Terminale S. Mais elles le sont encore à celui de Terminale STI2A...

[chan79]

Bonjour

Si on effectue l'homothétie de centre O et de rapport 2, alors et transformée en et (MP) en , qui est tangente à .
(MP) est parallèle à donc le milieu de [MP] est aligné avec O et I'. C'est I.
De même, J est le milieu de [MQ].

[Pseuda]

Bonjour,

Ok ! Ce qui me manquait, c'est "les milieux des cordes sont alignés avec le centre de l'ellipse et le point de tangence". J'aurais pu m'en douter au vu de la figure.