Ellipse dans rectangle tourné

[sylvain231]

Bonjour,
j'ai une question : j'ai une ellipse dont les 4 bords touchent un rectangle tourné. Ce rectangle a pour sommets P1, P2, P3, P4. On est dans le plan avec un repère orthonormé donc chacun des points est en (x,y).
Je cherche à calculer l'équation de l'ellipse qui est dans ce rectangle tourné (donc l'ellipse peut être tournée aussi).
Merci de votre aide.
Bonne journée

[Pisigma]

Bonjour,

qu'entends-tu par

j'ai une ellipse dont les 4 bords touchent un rectangle tourné

c'est quoi les bords d'une ellipse?

pourrais-tu joindre un dessin qui nous permettra de mieux comprendre?

[sylvain231]

en fait les axes doivent couper le milieu des côtés du rectangle

[Pisigma]

tu pars d'une figure horizontale constituée d'un rectangle et une ellipse ; ensuite tu cherches l'équation de l'ellipse quand la figure tourne d'un angle

l'ellipse horizontale a pour équation dans un système

et tu te demandes ce que devient l'équation de l'ellipse quand le système d'axes tourne de

C'est bien cela?

[catamat]

Bonjour

Si on ne veut pas changer de repère par rotation, on peut chercher les milieux A , B des petits côtés du rectangle, le milieu I de [AB] puis les longueurs des côtés du rectangle qui donneronnt a et b ce qui permet de calculer c par c²=a²-b².

Cela permet de placer les foyers F et F' sur le grand axe [AB] on a .

Enfin on obtient l'équation de l'ellipse qui est l'ensemble des M(x,y) tels que MF + MF'= 2a.

[sylvain231]

OK merci à vous deux je vais essayer

[sylvain231]

Rebonjour,
je préfère la réponse de catamat car elle demande moins de calculs, seulement catamat tu n'as pas précisé a est bien le côté long du rectangle et b son côté court, c'est bien cela ?

[catamat]

Oui a est le plus long.

[sylvain231]

OK merci avec tous ces renseignements je pense pouvoir me débrouiller

[sylvain231]

j'ai réussi mais j'ai dû changer quelques trucs :
c=sqrt(a²-b²)/2 à la place de c²=a²-b²
et
MF + MF'= a à la place de MF + MF'= 2a

[catamat]

Ok mais pour moi a était la moitié de la longueur du rectangle et b la moitié de la largeur.

[GaBuZoMeu]

Bonjour,
Plus marrant : trouver l'équation de l'ellipse inscrite dans le rectangle de sommets ( et réels 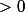) et tangente au côté gauche du rectangle au point d'ordonnée avec .

[sylvain231]

catamat : tu n'avais pas précisé que c'était les moitiés
merci à tous

[sylvain231]

mon sujet a été spammé on dirait

[GaBuZoMeu]

Hélas, l'administration est assez fantôme sur ce forum !