Element propre espace vectoriel des suites

[yoshi13]

Bonjour à tous ,

sur ce lien de cours : http://mp.cpgedupuydelome.fr/cours.php? ... rtie=77920

je ne comprends pas le tout dernier exemple de la page.

On cherche les valeurs propres de l'endomorphisme T, je ne vois pas le rapport avec "pour telle valeur la suite est bornée".
Du coup je ne comprends pas le vect(λ^n) qui décrit l'espace propre associé à la valeur λ.

D'après le cours, la méthode pour ce genre de question est :
Pour déterminer les valeurs propres de u, on étudie pour quels scalaires, λ∈K, l'équation
u(x)=λx possède d'autres solutions que la solution nulle.

Donc je ne comprends pas pourquoi on cherche à savoir quand la suite est-elle bornée.

Merci d'avance pour votre aide

Cordialement

[Kolis]

Bonjour !
Parce que l'exemple donné concerne l'espace des suites bornées !

[yoshi13]

Bonjour !
Parce que l'exemple donné concerne l'espace des suites bornées !

Bonjour Kolis,

Merci pour ta réponse, ca rend tout plus clair.

Je n'avais pas fait attention à la notation, pensant juste qu'il s'agissait des suites numériques à valeurs dans R.

Cependant j'ai encore un peu de mal avec le vect(λ^n).
( j'ai du mal à jongler avec l'espace vectoriel des suites :s )

Je n'arrive pas à concevoir ce que ce vect engendre.

Alors que par exemple il est ( pour moi ) beaucoup plus clair de comprendre ce qu'engendre un vect avec des vecteurs de R^n.

Merci d'avance

[Ben314]

Salut,
Ben c'est forcément plus compliqué vu que tu es en dimension infinie.
En dimension finie, on a systématiquement en tête le "point de vue géométrique" (celui de R^3) qui continue à donner une intuition à peu près correcte de ce qu'il se passe. Alors qu'avec l'infini, ben clairement l'intuition, ça risque plus de valoir grand chose.

Sinon, de façon pratique, déjà, c'est pas vect(λ^n) que tu est sensé écrire, mais le truc (bien plus lourd)
Regarde bien toutes les parenthèse et accolades qu'il y a là dedans et pourquoi elles sont là.
Et ce s.e.v. c'est en fait (par définition)
vu que (par définition)
C'est à dire l'ensemble de toutes les suites géométrique de raison (y compris la suite nulle)

[yoshi13]

Salut,
Ben c'est forcément plus compliqué vu que tu es en dimension infinie.
En dimension finie, on a systématiquement en tête le "point de vue géométrique" (celui de R^3) qui continue à donner une intuition à peu près correcte de ce qu'il se passe. Alors qu'avec l'infini, ben clairement l'intuition, ça risque plus de valoir grand chose.

Sinon, de façon pratique, déjà, c'est pas vect(λ^n) que tu est sensé écrire, mais le truc (bien plus lourd)
Regarde bien toutes les parenthèse et accolades qu'il y a là dedans et pourquoi elles sont là.
Et ce s.e.v. c'est en fait (par définition)
vu que (par définition)
C'est à dire l'ensemble de toutes les suites géométrique de raison (y compris la suite nulle)

Salut Ben314, merci pour ta réponse,

Oui tu as raison c'est plus rigoureux car ici les deux notations ne veulent vraiment pas dire la même chose.

Je comprends ce que tu veux dire, je vais continuer à me familiariser un peu avec les espaces infinis, par ailleurs, sur le même lien, l'exemple qui précède celui des suites , on a encore affaire à un espace infini, celui des fonctions infiniment dérivables.

Celui-là d'exemple je pense l'avoir compris, mais pour le vect, j'aurais plutôt écrit:

vect(x -> exp(λx) )

Je ne comprends pas trop la notation qu'ils ont donné avec Vect(e_λ) ou alors est-ce un abus de langage...

[Ben314]

A mon sens, il y a un très léger "abus de notation" qu'absolument tout le monde fait en écrivant vect() à la place de vect({}), mais il n'y a aucun "abus" du coté du vu que la ligne juste en dessous, ils définissent bien comme étant une fonction (de R dans C et qui est bien C^infinie) c'est à dire comme étant un élément de l'espace vectoriel considéré.
Tu peut bien sûr mettre à la place vect({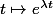}) vu que c'est exactement la même chose, mais ça me semble pas mal plus lisible sous la forme donnée dans le poly. où on a choisi de donner un nom à la fonction en question.

[yoshi13]

A mon sens, il y a un très léger "abus de notation" qu'absolument tout le monde fait en écrivant vect() à la place de vect({}), mais il n'y a aucun "abus" du coté du vu que la ligne juste en dessous, ils définissent bien comme étant une fonction (de R dans C et qui est bien C^infinie) c'est à dire comme étant un élément de l'espace vectoriel considéré.
Tu peut bien sûr mettre à la place vect({}) vu que c'est exactement la même chose, mais ça me semble pas mal plus lisible sous la forme donnée dans le poly. où on a choisi de donner un nom à la fonction en question.

D'accord au moins je suis sûr d'avoir compris, pas d'ambiguïté.
Merci Ben 314
bonne soirée