Bonjour,
Soit G un groupe muni de la loi x .
a,b sont des éléments de G tels que ba=ab² et ab=ba²
Montrer que a=b =e où e est le neutre de G.
j'ai essayé d'utiliser les symétriques et l'associativité (on n'a pas grand chose d'autre de toute façon) mais je ne parviens pas à m'en sortir. Merci pour votre aide !
Elément neutre
14 messages
- Page 1 sur 1
Re: Elément neutre
merci chan79. Je peux remplacer ensuite ba mais après ? quelle est la démarche ? Y-at-il une méthode pour mener à bien ce genre d'exercice ?
Re: Elément neutre
salut, l'idée c'est d'utiliser ce qu'on te donne!! ab=ba²=ba.a .
Modifié en dernier par jlb le 10 Déc 2017, 09:54, modifié 2 fois.
Re: Elément neutre
Salut,
Il faut uniquement essayer "d'emboiter" les différentes formules qu'on a pour en obtenir de nouvelles en essayant d'obtenir des trucs de plus en plus simple.
L'objectif étant bien évidement de se familiariser avec les "manipulation symboliques" dans un groupe donc je suis pas sûr du tout que ce soit un bon service à te rendre de faire l'exo. à ta place vu que ça veut dire qu'ensuite tu va partir avec un gros handicap...
Là, vu les deux formules que tu as, il y a deux trucs "évidents" qu'on doit penser à écrire.
Non, il n'y a pas de "recette magique" pour ce type d'exo.freezee a écrit:Y-at-il une méthode pour mener à bien ce genre d'exercice ?
Il faut uniquement essayer "d'emboiter" les différentes formules qu'on a pour en obtenir de nouvelles en essayant d'obtenir des trucs de plus en plus simple.
L'objectif étant bien évidement de se familiariser avec les "manipulation symboliques" dans un groupe donc je suis pas sûr du tout que ce soit un bon service à te rendre de faire l'exo. à ta place vu que ça veut dire qu'ensuite tu va partir avec un gros handicap...
Là, vu les deux formules que tu as, il y a deux trucs "évidents" qu'on doit penser à écrire.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Elément neutre
freezee a écrit:j'ai trouvé quelquechose
donc
donc a*b=e
donc
Tu as presque fini!! Si ab=e, reporte dans ba=ab² !!
Re: Elément neutre
Là, vu les deux formules que tu as, il y a deux trucs "évidents" qu'on doit penser à écrire
A ben314... si tu as une méthode différente pour résoudre cet exercice pourrais-tu me la soumettre ?
A ben314... si tu as une méthode différente pour résoudre cet exercice pourrais-tu me la soumettre ?
Re: Elément neutre
Perso, partant de  et
et 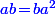 , ben le premier truc qui me vient à l'esprit, c'est "d'enquiller" les deux formules donc d'écrire que
, ben le premier truc qui me vient à l'esprit, c'est "d'enquiller" les deux formules donc d'écrire que 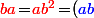b\!=\!({\blue ba^2})b\!=\!ba^2b) (la raison étant bien sûr le fait que les deux formules "inversent" l'ordre de a et de b, donc si on applique les deux, on se retrouve avec plus ou moins la même chose qu'au début)
(la raison étant bien sûr le fait que les deux formules "inversent" l'ordre de a et de b, donc si on applique les deux, on se retrouve avec plus ou moins la même chose qu'au début)
En multipliant à gauche par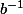 on en déduit que
on en déduit que  (que tu peut aussi écrire "en simplifiant à gauche par
(que tu peut aussi écrire "en simplifiant à gauche par  si tu as vu dans ton cours la notion "d'élément simplifiable à droite/à gauche")
si tu as vu dans ton cours la notion "d'élément simplifiable à droite/à gauche")
Puis, en multipliant à gauche par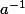 on en déduit que
on en déduit que 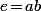 c'est à dire que
c'est à dire que 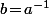
Et si on injecte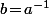 dans une des formules de départ, par exemple dans
dans une des formules de départ, par exemple dans 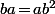 , ça donne
, ça donne 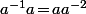 c'est à dire
c'est à dire 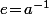 donc
donc 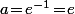 et on a aussi
et on a aussi 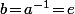 .
.
En multipliant à gauche par
Puis, en multipliant à gauche par
Et si on injecte
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Elément neutre
D'accord... merci à toi ben314.
j'avais une autre question également. A partir de l'égalité a.b=e peut-on conclure alors que a=e ou b=e et ensuite vérifier que si l'un deux éléments est l'élément neutre alors nécessairement l'autre est également l'élément neutre... est-ce correct ?
j'avais une autre question également. A partir de l'égalité a.b=e peut-on conclure alors que a=e ou b=e et ensuite vérifier que si l'un deux éléments est l'élément neutre alors nécessairement l'autre est également l'élément neutre... est-ce correct ?
Re: Elément neutre
Bien sûr... que non...freezee a écrit:A partir de l'égalité a.b=e peut-on conclure alors que a=e ou b=e...
Le fait que a.b=e, ce que ça te dit (dans un groupe de neutre e), c'est que b est l'inverse de a (et réciproquement) et absolument rien d'autre.
Par exemple, dans R* muni de la multiplication x (qui donne bien un groupe de neutre e=1), tu as 3 x (1/3) = 1 alors que ni 3 ni 1/3 ne sont égaux à 1 !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
