Égalité entre integrales

[allmess]

Bonjour !
Je rencontres des difficultés avec le problème suivant.. :==
Montrer que f=0 ou f=1

J'ai bien sûr pensé au théorème de Cauchy mais finalement je ne vois pas vraiment son utilité étant donné que l'on a déjà l'égalité des fonctions..
Si non il s'agirait il de montrer quelque chose du style f²=f, et si oui, comment ?

Merci d'avance

[zygomatique]

salut

et si tu étudiais leur différence ?

[allmess]

salut

et si tu étudiais leur différence ?

Merci
Alors à moins que je me soit égaré, par soustraction successives on montre qu'elles sont toutes égales à 0.. Comme la fonction f est continue (énoncé), si elle est de signe constant alors f=0
Si non elle s'annule au moins une fois..
Du coup je vois pas le f=1.. ^^

[wserdx]

As-tu essayé de développer ?

[allmess]

As-tu essayé de développer ?

Merci
Alors (f²-f)²=f;)-2f³+f>=0 (signe constant donc..)
Avec

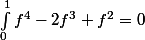
Et donc (f²-f)=0 D'où le résultat..?

[wserdx]

Merci
Alors (f²-f)²=f;)-2f³+f>=0 (signe constant donc..)
Avec

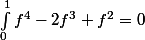
Et donc (f²-f)=0 D'où le résultat..?

oui si tu as une condition supplémentaire de continuité