Égalité avec sommes et intégrales

[Kyg]

Bonsoir

Je voudrais montrer que

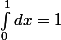
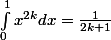
Sachant que et , étant un entier naturel non nul.

[Robot]

[Kyg]

Je ne trouve pas...

[Robot]

Commence avec des petites valeurs de n.
Pour n=0 ?
Pour n=1 ?
Pour n=2 ?

Remarque : la réponse est cachée dans le résultat à montrer et l'indication qui est donnée. Elémentaire, mon cher Watson ! :lol3:

[Kyg]

Après maints essais je n'y arrive toujours pas, je me suis avancée sur une autre piste qui me paraît exploitable mais je suis encore bloquée :

[Pythales]

Après maints essais je n'y arrive toujours pas, je me suis avancée sur une autre piste qui me paraît exploitable mais je suis encore bloquée :

Tu verrais peut-être mieux les choses si tu écrivais

[zygomatique]

salut

pourtant Robot a donné une bonne indication ...



:lol3:

[Robot]

Kyg, je suis sûr que tu n'as pas essayé de remplacer le point d'interrogation dans pour n=0, 1, 2.

[Kyg]

Si mais je ne comprends vraiment pas pourquoi peut s'écrire sous la forme d'un produit de sommes !

[Robot]

Si tu l'as fait, qu'as-tu trouvé ?
Les identités qui donnent des factorisations, comme par exemple , tu n'as jamais vu ?

[Kyg]

Ce travail est à rendre pour demain et je ne saisis toujours pas cette piste... Je ne comprends vraiment rien et je ne vois pas d'identité remarquable. Est-ce que la piste que j'ai donné précédemment marche sinon ? Comment la continuer ?

[Sake]

Salut,

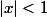
Développe avec pour voir...

Edit : Pour la somme partielle, on n'a pas besoin de |x| < 1, bien sûr, tant que x est différent de 1...

[Kyg]

Merci à tous pour vos réponses, j'ai finalement trouvé un moyen d'y parvenir à partir de ce que j'avais fait et simplement en multipliant l'intérieur de l'intégrale par !

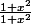
[Sake]

Merci à tous pour vos réponses, j'ai finalement trouvé un moyen d'y parvenir à partir de ce que j'avais fait et simplement en multipliant l'intérieur de l'intégrale par !

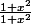
Ben en fait il fallait pas se casser la tête. Tout t'est donné dans l'énoncé.

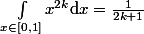
On te dit que , donc et comme ici il s'agit d'une somme discrète d'un nombre fini de termes, on intervertit les symboles et sans problème, ce qui donne :