EDP: recherche de solutions particulières avec conditions au

par **egan** » 31 Oct 2010, 18:37

Salut tout le monde,
J'ai réfléchi un peu au problème suivant mais je ne vois pas comment faire.
Soit

une fonction

vérifiant l'EDP suivante:

La solution générale de cette EDP est:

où

Je voudrais trouver toutes les solutions vérifiant:

Mais je coince. Je m'en remets donc à vous.
Merci d'avance.
@+ Boris.

par **girdav** » 31 Oct 2010, 18:49

Pourquoi ne pas prendre

?

par **egan** » 01 Nov 2010, 13:20

Oui oui je suis d'accord mais je voudrais trouver toutes les solutions vérifiant ces conditions.

par **Matt_01** » 01 Nov 2010, 13:26

Eh bien c'est justement la seule.

par **girdav** » 01 Nov 2010, 13:42

On peut vérifier l'unicité : si f et g sont deux solutions telles que

,

et

,

pour tous

et

alors

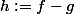
est de la forme

et le fait que

pour tout

montre que

.

par **Matt_01** » 01 Nov 2010, 13:53

On a aussi

sur

donc