EDP d'ordre 1
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Menethan
- Messages: 3
- Enregistré le: 08 Déc 2017, 17:28
-
 par Menethan » 08 Déc 2017, 17:40
par Menethan » 08 Déc 2017, 17:40
Bonjour à tous,
Je cale sur la résolution de l'EDP suivante (avec u simplement

):
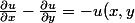 +x + f(y))
Où

est une fonction quelconque de y.
Avec le changement de variable classique
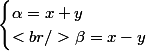
Je la transforme en :
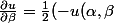 + (\frac{\alpha +\beta }{2}) + f(\frac{\alpha -\beta }{2})))
Mais je ne suis pas sur que cela m'avance à grand chose... Du coup je ne trouve pas d'autres pistes (la méthode des caractéristiques ne semblant pas marcher non plus...)
NB : A la base, l'exercice consiste à résoudre l'EDP d'ordre 2 :
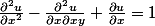
Et j'arrive à mon équation avec
)
en "factorisant" le

Peut-être y a-t-il une autre façon de procéder avec l'EDP de départ ?
-
Menethan
- Messages: 3
- Enregistré le: 08 Déc 2017, 17:28
-
 par Menethan » 08 Déc 2017, 18:55
par Menethan » 08 Déc 2017, 18:55
Edit : j'ai modifié mon départ suite au message de Ben314 car sans ça ce n'était effectivement pas clair. Du coup, f(y) est que c'est un résultat d'intégration.
-
Menethan
- Messages: 3
- Enregistré le: 08 Déc 2017, 17:28
-
 par Menethan » 08 Déc 2017, 20:30
par Menethan » 08 Déc 2017, 20:30
Problème résolu, le topic peut être fermé, désolé du dérangement !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Déc 2017, 21:43
par Ben314 » 08 Déc 2017, 21:43
Menethan a écrit:Edit : j'ai modifié mon départ suite au message de Ben314 car sans ça ce n'était effectivement pas clair. Du coup, f(y) est que c'est un résultat d'intégration.
Et moi, j'aivais précédement enlevé le mien vu que le "N.B." final expliquant d'où provenait l'équation donnait la réponse à la question que je me posait concernant la "nature" du f de l'E.D.P..
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
