Ecriture matricielle

[rhosmah]

Bonsoir,

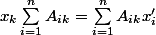
j'aurais besoin d'écrire le système d'équations (k=1,...,m) sous forme matricielle, où
A est une matrice nxm
x' est un vecteur colonne nx1
x est un vecteur colonne mx1

Pour le membre de droite, je pense que c'est simplement , mais j'ai l'impression que le membre de gauche ne peut pas s'écrire sous forme matricielle. Pouvez-vous m'aider ? Merci!

[fatal_error]

salut,

pour le membre de gauche, tu peux considérer le vecteur 1
de dimension 1xn
soit x_k 1 A_{:,k}
A_{:,k} représentant le vecteur de la kieme colonne de A.

[rhosmah]

salut,

pour le membre de gauche, tu peux considérer le vecteur 1
de dimension 1xn
soit x_k 1 A_{:,k}
A_{:,k} représentant le vecteur de la kieme colonne de A.

Merci pour ta réponse, mais n'y a-t-il pas un moyen d'écrire cela sans "bidouiller" avec un vecteur A_{:,k} ? J'entends par là: avoir une expression où n'apparaissent que A, x, et éventuellement des matrices remplies de 1 ?

[fatal_error]

ben si tu veux pas modifier A, tu enquilles une matrice alacon pour recuperer le kieme vecteur genre
[0 - 1 - 0] avec 1 en kieme position
t'écris alors
x_k 1 A [0 - 1 - 0]'

cela dit je sais pas si ca répond a ta question. Je vois pas trop la finalité de la chose.

[rhosmah]

ben si tu veux pas modifier A, tu enquilles une matrice alacon pour recuperer le kieme vecteur genre
[0 - 1 - 0] avec 1 en kieme position
t'écris alors
x_k 1 A [0 - 1 - 0]'

cela dit je sais pas si ca répond a ta question. Je vois pas trop la finalité de la chose.

Il me faudrait une expression où n'apparaisse pas k... Il s'agit d'un système de m équations, le k que j'ai écris ici veut juste dire qu'on a x_k à la kème équation du système. k n'est pas une donnée du problème.

[fatal_error]

qqch comme
(1 A) I_n x
alors...
1_n A fait la somme pour chaque colonne de A dans un vecteur 1,m
(1AI_n) est une matrice diagonale, dont la valeur a la ieme ligne est le ieme elem de 1A
enfin x est le vecteur m,1
et le produit (1AI_n)x multiplie le kieme elem de x par le kieme coeff de 1AI_n qui est la somme de la kieme colonne de A

[rhosmah]

qqch comme
(1 A) I_n x
alors...
1_n A fait la somme pour chaque colonne de A dans un vecteur 1,m
(1AI_n) est une matrice diagonale, dont la valeur a la ieme ligne est le ieme elem de 1A
enfin x est le vecteur m,1
et le produit (1AI_n)x multiplie le kieme elem de x par le kieme coeff de 1AI_n qui est la somme de la kieme colonne de A

Il y a un problème: le vecteur ligne 1_n multiplié par A donne une matrice 1xm, je ne vois pas comment tu multiplies cela avec I_n qui est une matrice nxn...

[fatal_error]

l'idée c'est de transformer le vecteur en une matrice pour préserver après l'écriture matricielle.

Si t'as un vecteur 1xm, ben tu multiplies par I_m.

ok une faute de frappe, mais faut pas s'attarder trop sur les détails avec moi, c'est écrit dans mon pseudo.

[fatal_error]

ouais en fait la difficulté dans mon approche réside en transformer le vecteur
1,m en matrice m,m diagonale

[fatal_error]

finalement abandonné, on peut s'en sortir avec ce lien mais c'est pas très sexy