Echange des signes limites

par **jacques770** » 14 Mar 2008, 13:09

J'ai

puis

et je cherche à échanger les signes limites entre $n$ et $k$,
sachant que $f$ et les $f_k$ sont des densités.

Merci

par **alavacommejetepousse** » 14 Mar 2008, 13:11

bonjour

peux tu réecrire ?

par **jacques770** » 14 Mar 2008, 13:17

c'est fait !!

par **alavacommejetepousse** » 14 Mar 2008, 13:30

à n fixé les f n,k ont elles par hypothèse une limite g n quand k tend vers l'infini ?

par **jacques770** » 14 Mar 2008, 13:43

non hélas rien à priori...

par **alavacommejetepousse** » 14 Mar 2008, 13:55

sur [0,1/2]

fn,k(x) = k x^n

vérifie tes hypothèses
et la limite à n fixé pour k->+infini n 'existe pas donc la question de l 'interversion pas plus.

par **jacques770** » 14 Mar 2008, 14:05

Je penchais plutot vers une convergence uniforme en k des

,
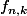
j'ai vérifié le contre exemple, il ne vérifie pas les conditions.

par **alavacommejetepousse** » 14 Mar 2008, 16:05

heu
quelle condition est non vérifiée?

par **Dominique Lefebvre** » 14 Mar 2008, 17:20

jacques770 a écrit:J'ai

puis

et je cherche à échanger les signes limites entre $n$ et $k$,
sachant que $f$ et les $f_k$ sont des densités.

Merci

Bonjour,
La politesse n'est pas une option sur notre forum! Je te prie de vouloir bien lire le règlement et la politique du forum.

Pour la modération

par **alavacommejetepousse** » 14 Mar 2008, 18:41

Dominique Lefebvre a écrit:Bonjour,
La politesse n'est pas une option sur notre forum! Je te prie de vouloir bien lire le règlement et la politique du forum.

Pour la modération

Salut Camarade toujours dans l'axe.

Echange des signes limites

Echange des signes limites

Qui est en ligne